Vector spaces | Mathematical structures | Vectors (mathematics and physics) | Group theory
Vector space
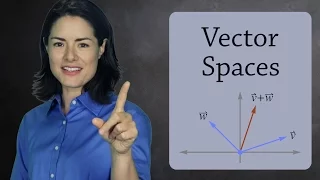
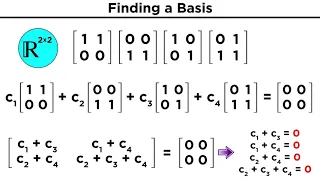
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called vectors, may be added together and multiplied ("scaled") by numbers called scalars. Scalars are often real numbers, but can be complex numbers or, more generally, elements of any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called vector axioms. The terms real vector space and complex vector space are often used to specify the nature of the scalars: real coordinate space or complex coordinate space. Vector spaces generalize Euclidean vectors, which allow modeling of physical quantities, such as forces and velocity, that have not only a magnitude, but also a direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix, which allows computing in vector spaces. This provides a concise and synthetic way for manipulating and studying systems of linear equations. Vector spaces are characterized by their dimension, which, roughly speaking, specifies the number of independent directions in the space. This means that, for two vector spaces with the same dimension, the properties that depend only on the vector-space structure are exactly the same (technically the vector spaces are isomorphic). A vector space is finite-dimensional if its dimension is a natural number. Otherwise, it is infinite-dimensional, and its dimension is an infinite cardinal. Finite-dimensional vector spaces occur naturally in geometry and related areas. Infinite-dimensional vector spaces occur in many areas of mathematics. For example, polynomial rings are countably infinite-dimensional vector spaces, and many function spaces have the cardinality of the continuum as a dimension. Many vector spaces that are considered in mathematics are also endowed with other structures. This is the case of algebras, which include field extensions, polynomial rings, associative algebras and Lie algebras. This is also the case of topological vector spaces, which include function spaces, inner product spaces, normed spaces, Hilbert spaces and Banach spaces. (Wikipedia).