
in this video we look at basic properties of algebra
From playlist Skill 7 Attempt 1

Sets might contain an element that can be identified as an identity element under some binary operation. Performing the operation between the identity element and any arbitrary element in the set must result in the arbitrary element. An example is the identity element for the binary opera
From playlist Abstract algebra

in this video we look at basic properties of algebra
From playlist Skill 7 Attempt 2

Determine the Additive Inverses
This video explains how to determine the additive inverse of a given integers. http://mathispower4u.com
From playlist Sets of Numbers/Properties of Real Numbers
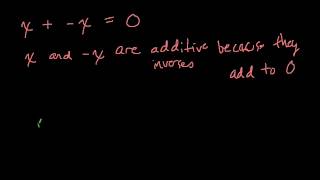
#15 additive inverse - integrated algebra June 2009 #26
An example dealing with the additive inverse
From playlist Integrated Algebra Regents 2008-2009

In this problem we look at several examples of additive inverses
From playlist Middle School This Year

The Additive Group of Integers Modulo n
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The Additive Group of Integers Modulo n
From playlist Abstract Algebra

Discrete Math - 2.2.2 Set Identities
Identity, domination idempotent, complementation, commutative, associative, distributive, De Morgan, absorption and complement laws for sets. Textbook: Rosen, Discrete Mathematics and Its Applications, 7e Playlist: https://www.youtube.com/playlist?list=PLl-gb0E4MII28GykmtuBXNUNoej-vY5Rz
From playlist Discrete Math I (Entire Course)

A set might contain many inverse elements under some binary operation. To have such an element, this set must also contain an identity element under the binary operation in question. An element is an inverse element of another element in a set if performing the binary operation between t
From playlist Abstract algebra

Definition of a Ring and Examples of Rings
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Ring and Examples of Rings - Definition of a Ring. - Definition of a commutative ring and a ring with identity. - Examples of Rings include: Z, Q, R, C under regular addition and multiplication The Ring of all n x
From playlist Abstract Algebra
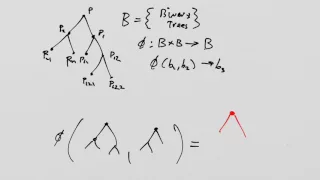
What is a Tensor? Lesson 19: Algebraic Structures I
What is a Tensor? Lesson 19: Algebraic Structures Part One: Groupoids to Fields This is a redo or a recently posted lesson. Same content, a bit cleaner. Algebraic structures are frequently mentioned in the literature of general relativity, so it is good to understand the basic lexicon of
From playlist What is a Tensor?

Identities and Inverses // Math Minute [#3] [ALGEBRA]
In algebra, it's often useful to be able to "undo" things, operations, functions, etc., so we need an object called an inverse. But we also need to understand what that inverse is "undoing" us back to. So that's where identities come in. I look here at the additive identity and the multipl
From playlist Math Minutes

Abstract Algebra - 2.1 Definition and Examples of Groups
In this video we explore each of the 4 properties that must be satisfied for a set to be a group for a given operation. Each property will have an example and a non-example to explain how a property can be met or not met. Video Chapters: Intro 0:00 Closure 0:14 Associativity 2:39 Identit
From playlist Abstract Algebra - Entire Course

Alison Etheridge & Nick Barton: Applying the infinitesimal model
The infinitesimal model is based on the assumption that, conditional on the pedigree, the joint distribution of trait values is multivariate normal, then, selecting parents does not alter the variance amongst offspring. We explain how the infinitesimal model extends to include dominance as
From playlist Probability and Statistics

Algebraic Structures: Groups, Rings, and Fields
This video covers the definitions for some basic algebraic structures, including groups and rings. I give examples of each and discuss how to verify the properties for each type of structure.
From playlist Abstract Algebra

How to use PROPERTIES of REAL NUMBERS - COLLEGE ALGEBRA
We talk about properties of real numbers in college algebra: commutativity, associativity, distributivity, identity, and inverses. 00:00 Intro 00:40 Commutativity 02:33 Associativity 04:29 Distributivity 08:09 Identity 09:45 Inverse 12:40 Subtraction and Division is Addition and Multiplic
From playlist College Algebra

Rings and Fields -- Abstract Linear Algebra 5
⭐Highly Suggested Linear Algebra books⭐ Linear Algebra, an introduction to abstract mathematics: https://amzn.to/3rkp4Wc Linear Algebra Done Right: https://amzn.to/3rkp4Wc The Manga Guide to Linear Algebra: https://amzn.to/3HnS59o A First Course in Linear Algebra: http://linear.ups.edu/ Li
From playlist Abstract Linear Algebra

Oxford Linear Algebra: What is a Vector Space?
University of Oxford mathematician Dr Tom Crawford explains the vector space axioms with concrete examples. Check out ProPrep with a 30-day free trial to see how it can help you to improve your performance in STEM-based subjects: https://www.proprep.uk/info/TOM-Crawford Test your under
From playlist Oxford Linear Algebra

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra
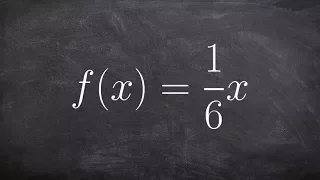
Learn how to find inverse of a function and determine if the inverse is a function or not
👉 Learn how to find the inverse of a linear function. A linear function is a function whose highest exponent in the variable(s) is 1. The inverse of a function is a function that reverses the "effect" of the original function. One important property of the inverse of a function is that whe
From playlist Find the Inverse of a Function