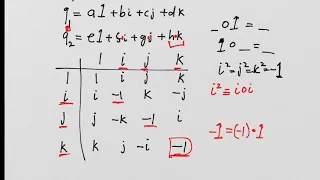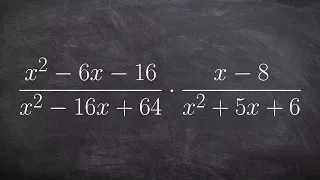Composition algebras | Quaternions
Quaternion
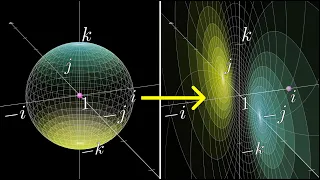
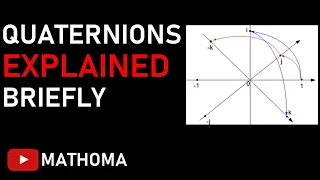
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space, or, equivalently, as the quotient of two vectors. Multiplication of quaternions is noncommutative. Quaternions are generally represented in the form where a, b, c, and d are real numbers; and i, j, and k are the basic quaternions. Quaternions are used in pure mathematics, but also have practical uses in applied mathematics, particularly for calculations involving three-dimensional rotations, such as in three-dimensional computer graphics, computer vision, and crystallographic texture analysis. They can be used alongside other methods of rotation, such as Euler angles and rotation matrices, or as an alternative to them, depending on the application. In modern mathematical language, quaternions form a four-dimensional associative normed division algebra over the real numbers, and therefore a ring, being both a division ring and a domain. The algebra of quaternions is often denoted by H (for Hamilton), or in blackboard bold by It can also be given by the Clifford algebra classifications In fact, it was the first noncommutative division algebra to be discovered. According to the Frobenius theorem, the algebra is one of only two finite-dimensional division rings containing a proper subring isomorphic to the real numbers; the other being the complex numbers. These rings are also Euclidean Hurwitz algebras, of which the quaternions are the largest associative algebra (and hence the largest ring). Further extending the quaternions yields the non-associative octonions, which is the last normed division algebra over the real numbers. (The sedenions, the extension of the octonions, have zero divisors and so cannot be a normed division algebra.) The unit quaternions can be thought of as a choice of a group structure on the 3-sphere S3 that gives the group Spin(3), which is isomorphic to SU(2) and also to the universal cover of SO(3). (Wikipedia).