
Field Theory - Algebraically Closed Fields - Lecture 9
In this video we define what an algebraically closed field and assert without proof that they exist. We also explain why if you can find a single root for any polynomial, then you can find them all.
From playlist Field Theory

Field Theory - Algebraically Closed Fields (part 2) - Lecture 10
In this video we should that algebraically closed fields exist and are unique. We assume that the direct limit construction works. The construction here depends on the axiom of choice.
From playlist Field Theory

Galois theory: Algebraic closure
This lecture is part of an online graduate course on Galois theory. We define the algebraic closure of a field as a sort of splitting field of all polynomials, and check that it is algebraically closed. We hen give a topological proof that the field C of complex numbers is algebraically
From playlist Galois theory

FIT2.3.3. Algebraic Extensions
Field Theory: We define an algebraic extension of a field F and show that successive algebraic extensions are also algebraic. This gives a useful criterion for checking algberaic elements. We finish with algebraic closures.
From playlist Abstract Algebra
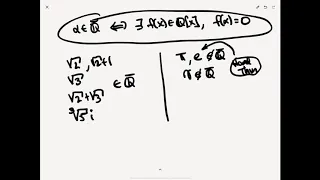
Field Theory -- Qbar, the field of algebraic numbers -- Lecture 8
In this video we show that QQbar, the algebraic closure of the rational numbers is countable.
From playlist Field Theory

algebraic geometry 30 The Ax Grothendieck theorem
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the Ax-Grothendieck theorem, which states that an injective regular map between varieties is surjective. The proof uses a strange technique: first prove the resu
From playlist Algebraic geometry I: Varieties

algebraic geometry 29 Automorphisms of space
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It describes the automorphisms of affine and projective space, and gives a brief discussion of the Jacobian conjecture.
From playlist Algebraic geometry I: Varieties

algebraic geometry 24 Regular functions
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers regular functions on affine and quasiprojective varieties.
From playlist Algebraic geometry I: Varieties

Definition of a Field In this video, I define the concept of a field, which is basically any set where you can add, subtract, add, and divide things. Then I show some neat properties that have to be true in fields. Enjoy! What is an Ordered Field: https://youtu.be/6mc5E6x7FMQ Check out
From playlist Real Numbers

Multi-valued algebraically closed fields are NTP₂ - W. Johnson - Workshop 2 - CEB T1 2018
Will Johnson (Niantic) / 05.03.2018 Multi-valued algebraically closed fields are NTP₂. Consider the expansion of an algebraically closed field K by 𝑛 arbitrary valuation rings (encoded as unary predicates). We show that the resulting structure does not have the second tree property, and
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields
Title: Differential Fields—A Model Theorist's View May 2016 Kolchin Seminar Workshop
From playlist May 2016 Kolchin Seminar Workshop

Daniel Hoffmann, University of Warsaw
May 14, Daniel Hoffmann, University of Warsaw Fields with derivations and action of finite group
From playlist Spring 2021 Online Kolchin Seminar in Differential Algebra

On a Hecke algebra isomorphism of Kazhdan by Radhika Ganapathy
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Omar Leon Sanchez University of Manchester Differentially large fields Recall that a field K is large if it is existentially closed in the field of Laurent series K((t)). Examples of such fields are the complex, the real, and the p-adic numbers. This class of fields has been exploited si
From playlist Fall 2019 Kolchin Seminar in Differential Algebra

Finiteness theorems for Kolchin's constrained cohomology
By Anand Pillay, University of Notre Dame Finiteness theorems for Kolchin's constrained cohomology Kolchin Seminar, CUNY Graduate Center, October 4, 2019
From playlist Fall 2019 Kolchin Seminar in Differential Algebra

Title: The Dixmier-Moeglin Problem for D-Varieties May 2016 Kolchin Seminar Workshop
From playlist May 2016 Kolchin Seminar Workshop

Field Theory: We consider the property of algebraic in terms of finite degree, and we define algebraic numbers as those complex numbers that are algebraic over the rationals. Then we give an overview of algebraic numbers with examples.
From playlist Abstract Algebra

Strongly minimal groups in o-minimal structures - K. Peterzil - Workshop 3 - CEB T1 2018
Kobi Peterzil (Haifa) / 27.03.2018 Strongly minimal groups in o-minimal structures Let G be a definable two-dimensional group in an o-minimal structure M and let D be a strongly minimal expansion of G, whose atomic relations are definable in M. We prove that if D is not locally modular t
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields