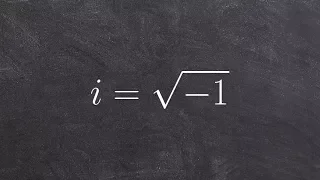Elementary mathematics | Real numbers | Real algebraic geometry
Real number
In mathematics, a real number is a number that can be used to measure a continuous one-dimensional quantity such as a distance, duration or temperature. Here, continuous means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers is denoted R or and is sometimes called "the reals".The adjective real in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of −1), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers include the rational numbers, such as the integer −5 and the fraction 4 / 3. The rest of the real numbers are called irrational numbers, and include algebraic numbers (such as the square root √2 = 1.414...) and transcendental numbers (such as π = 3.1415...). Real numbers can be thought of as all points on an infinitely long line called the number line or real line, where the points corresponding to integers (..., −2, −1, 0, 1, 2, ...) are equally spaced. Conversely, analytic geometry is the association of points on lines (especially axis lines) to real numbers such that geometric displacements are proportional to differences between corresponding numbers. The informal descriptions above of the real numbers are not sufficient for ensuring the correctness of proofs of theorems involving real numbers. The realization that a better definition was needed, and the elaboration of such a definition was a major development of 19th-century mathematics and is the foundation of real analysis, the study of real functions and real-valued sequences. A current axiomatic definition is that real numbers form the unique (up to an isomorphism) Dedekind-complete ordered field. Other common definitions of real numbers include equivalence classes of Cauchy sequences (of rational numbers), Dedekind cuts, and infinite decimal representations. All these definitions satisfy the axiomatic definition and are thus equivalent. (Wikipedia).