Elementary mathematics | Functions and mappings | Basic concepts in set theory
Function (mathematics)
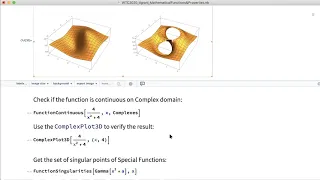
In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function. The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a function of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly enlarged the domains of application of the concept. A function is most often denoted by letters such as f, g and h, and the value of a function f at an element x of its domain is denoted by f(x); the numerical value resulting from the function evaluation at a particular input value is denoted by replacing x with this value; for example, the value of f at x = 4 is denoted by f(4). When the function is not named and is represented by an expression E, the value of the function at, say, x = 4 may be denoted by E|x=4. For example, the value at 4 of the function that maps x to may be denoted by (which results in 25). A function is uniquely represented by the set of all pairs (x, f (x)), called the graph of the function, a popular means of illustrating the function. When the domain and the codomain are sets of real numbers, each such pair may be thought of as the Cartesian coordinates of a point in the plane. Functions are widely used in science, engineering, and in most fields of mathematics. It has been said that functions are "the central objects of investigation" in most fields of mathematics. (Wikipedia).