Geometry
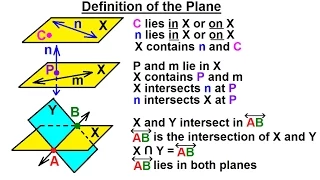
Geometry (from Ancient Greek γεωμετρία (geōmetría) 'land measurement'; from γῆ (gê) 'earth, land', and μέτρον (métron) 'a measure') is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a geometer. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Gauss' Theorema Egregium ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied intrinsically, that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries without the parallel postulate (non-Euclidean geometries) can be developed without introducing any contradiction. The geometry that underlies general relativity is a famous application of non-Euclidean geometry. Since then, the scope of geometry has been greatly expanded, and the field has been split in many subfields that depend on the underlying methods—differential geometry, algebraic geometry, computational geometry, algebraic topology, discrete geometry (also known as combinatorial geometry), etc.—or on the properties of Euclidean spaces that are disregarded—projective geometry that consider only alignment of points but not distance and parallelism, affine geometry that omits the concept of angle and distance, finite geometry that omits continuity, and others. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, a problem that was stated in terms of elementary arithmetic, and remained unsolved for several centuries. (Wikipedia).