Modular arithmetic | Finite rings | Group theory
Modular arithmetic
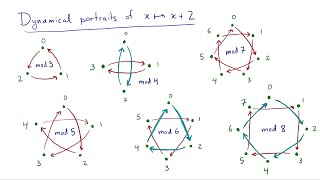
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae, published in 1801. A familiar use of modular arithmetic is in the 12-hour clock, in which the day is divided into two 12-hour periods. If the time is 7:00 now, then 8 hours later it will be 3:00. Simple addition would result in 7 + 8 = 15, but clocks "wrap around" every 12 hours. Because the hour number starts over at zero when it reaches 12, this is arithmetic modulo 12. In terms of the definition below, 15 is congruent to 3 modulo 12, so "15:00" on a 24-hour clock is displayed "3:00" on a 12-hour clock. (Wikipedia).