
Trigonometric Identities (1 of 3: Reciprocals, Ratios & Complements)
More resources available at www.misterwootube.com
From playlist Trigonometric Functions and Identities

Quadratic Identities (1 of 2: By comparison of coefficients)
More resources available at www.misterwootube.com
From playlist Polynomials (related content)

Verifying Trigonometric Identities: The Fundamental Identities
Visit http://mathispower4u.wordpress.com/ for a categorized and searchable list of all videos.
From playlist Reciprocal, Quotient, Negative, and Pythagorean Trigonometric Identities

Compound Angle Identities (1 of 3: Proving sin(a+b) geometrically)
More resources available at www.misterwootube.com
From playlist Further Trigonometric Identities

Cubic Identities (1 of 3: What is an identity?)
More resources available at www.misterwootube.com
From playlist Further Equations
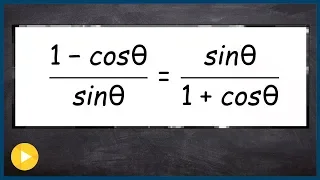
Verify an identity by multiplying by the conjugate
👉 Learn how to verify Pythagoras trigonometric identities. A Pythagoras trigonometric identity is a trigonometric identity of the form sin^2 (x) + cos^2 (x) or any of its derivations. To verify trigonometric expression means to verify that the term(s) on the left-hand side of the equality
From playlist Verify Trigonometric Identities

How to verify a trigonometric identity by factoring
👉 Learn how to verify Pythagoras trigonometric identities. A Pythagoras trigonometric identity is a trigonometric identity of the form sin^2 (x) + cos^2 (x) or any of its derivations. To verify trigonometric expression means to verify that the term(s) on the left-hand side of the equality
From playlist Verify Trigonometric Identities

Quadratic Identities (3 of 4: Comparing Coefficients)
More resources available at www.misterwootube.com
From playlist Working with Functions (related content)

Verify trig identities with multiple identities
👉 Learn how to verify Pythagoras trigonometric identities. A Pythagoras trigonometric identity is a trigonometric identity of the form sin^2 (x) + cos^2 (x) or any of its derivations. To verify trigonometric expression means to verify that the term(s) on the left-hand side of the equality
From playlist Verify Trigonometric Identities

301.2B Basic Properties of Groups
A group in abstract algebra is a relatively simple structure — but in this video we see how that simple structure enables us to do a lot of what we understand as basic algebra, such as solving equations via cancellation, and having unique identity and inverses.
From playlist Modern Algebra

GT18. Conjugacy and The Class Equation
Abstract Algebra: We consider the group action of the group G on itself given by conjugation. The orbits, called conjugacy classes, partition the group, and we have the Class Equation when G is finite. We also show that the partition applies to normal subgroups. Finally we apply the cla
From playlist Abstract Algebra
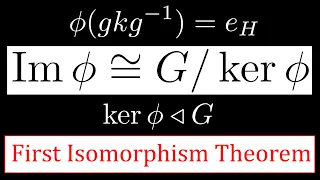
Kernel and First Isomorphism Theorem - Group Theory
0:00 Kernel is a Normal Subgroup 5:20 First Isomorphism Theorem The first isomorphism theorem is a fundamental theorem in group theory that gives us a powerful way to find isomorphic groups. In this video, we explain what the kernel of a homomorphism is and how to turn a homomorphism into
From playlist Group Theory

Visual Group Theory, Lecture 4.2: Kernels
Visual Group Theory, Lecture 4.2: Kernels The kernel of a homomorphism is the set of elements that get mapped to the identity. We show that it is always a normal subgroup of the domain, and that the preimages of the other elements are its cosets. This means that we can always quotient out
From playlist Visual Group Theory
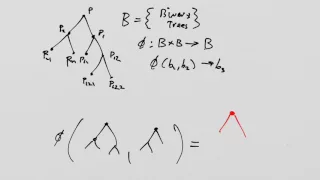
What is a Tensor? Lesson 19: Algebraic Structures I
What is a Tensor? Lesson 19: Algebraic Structures Part One: Groupoids to Fields This is a redo or a recently posted lesson. Same content, a bit cleaner. Algebraic structures are frequently mentioned in the literature of general relativity, so it is good to understand the basic lexicon of
From playlist What is a Tensor?

Representation theory: Frobenius groups
We recall the definition of a Frobenius group as a transitive permutation group such that any element fixing two points is the identity. Then we prove Frobenius's theorem that the identity together with the elements fixing no points is a normal subgroup. The proof uses induced representati
From playlist Representation theory
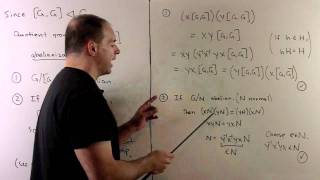
EDIT: At 11:50, r^2(l-k) should be r^2l. At 14:05, index for top one should be n-2, not 2n-2. Abstract Algebra: We define the commutator subgroup for a group G and the corresponding quotient group, the abelianization of G. The main example is the dihedral group, which splits into tw
From playlist Abstract Algebra

GT10. Examples of Non-Isomorphic Groups
EDIT: Fix for 14:10: "Here's a quick way to fix. If y has order 3, then the order of yH divides 3. By assumption, yH has order 2, a contradiction. Recall that yH=H means y is in H. I'm actually overthinking the entire proof. Once we have H, pick any y not in H. Then yxy^-1=x^2.
From playlist Abstract Algebra

Definition of a Group and Examples of Groups
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Group and Examples of Groups
From playlist Abstract Algebra

Simplify a trig expression by multiplying by the LCD
👉 Learn how to simplify trigonometric expressions by factoring, expansion, and re-grouping. To simplify a trigonometric identity means to reduce the identity to the simplest form it can take which may be a number or a simple trigonometric function. This can be achieved by various means i
From playlist How to Simplify The Trigonometric Identities by Dividing

Solving Hard Exams - Algebra and Arithmetic Exercise 1 - Group Theory, Normal Subgroups, Matrices
Help me create more free content! =) https://www.patreon.com/mathable Merch :v - https://teespring.com/stores/papaflammy https://www.amazon.com/shop/flammablemaths https://shop.spreadshirt.de/papaflammy Become a Member of the Flammily! :0 https:
From playlist Solving Hard Exams!