
Associative Binary Operations and Examples Video
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Associative Binary Operations and Examples Video. This is video 2 on Binary Operations.
From playlist Abstract Algebra

Determine if the Binary Operation Defined by the Table is Commutative and Associative
In this video we determine whether or not a binary operation is commutative and associative. The binary operation is actually defined by a table in this example. I hope this video helps someone.
From playlist Abstract Algebra

In this exercise problem we prove the associative property of the intersection of three sets.
From playlist Abstract algebra

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra

Definition of a Group and Examples of Groups
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Group and Examples of Groups
From playlist Abstract Algebra

19 Defining the types of binary operations
The two types of binary operations discussed in this video are commutative and associative. We saw them in the previous video and here we define them specifically so that we can build on our repertoire to use in proofs. Remember, it is by filling up our toolbox with these definitions that
From playlist Abstract algebra

The most misunderstood equation in math (associative property)
Associativity is one of the first properties taught to students. Let's explore this property together. For the curious among you, the mathematical theorem at the heart of this video is Cayley’s theorem for semigroups. 00:00 The equation 02:20 Exploration 13:36 What is associativity? Part
From playlist Summer of Math Exposition Youtube Videos

A gentle description of a vertex algebra.
Working from the notions of associative algebras, Lie algebras, and Poisson algebras we build the idea of a vertex algebra. We end with the proper definition as well as an "intuition" for how to think of the parts. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation
From playlist Vertex Operator Algebras

Semisimple $\mathbb{Q}$-algebras in algebraic combinatorics by Allen Herman
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Representation theory of W-algebras and Higgs branch conjecture – Tomoyuki Arakawa – ICM2018
Lie Theory and Generalizations Invited Lecture 7.2 Representation theory of W-algebras and Higgs branch conjecture Tomoyuki Arakawa Abstract: We survey a number of results regarding the representation theory of W-algebras and their connection with the resent development of the four dimen
From playlist Lie Theory and Generalizations

L. Boyle: Non-commutative geometry, non-associative geometry, and the std. model of particle physics
Connes' notion of non-commutative geometry (NCG) generalizes Riemannian geometry and yields a striking reinterepretation of the standard model of particle physics, coupled to Einstein gravity. We suggest a simple reformulation with two key mathematical advantages: (i) it unifies many of t
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Pre-recorded lecture 9: Homogeneous linear Nijenhuis operators and left-symmetric algebras
MATRIX-SMRI Symposium: Nijenhuis Geometry and integrable systems Pre-recorded lecture: These lectures were recorded as part of a cooperation between the Chinese-Russian Mathematical Center (Beijing) and the Moscow Center of Fundamental and Applied Mathematics (Moscow). Nijenhuis Geomet
From playlist MATRIX-SMRI Symposium: Nijenhuis Geometry companion lectures (Sino-Russian Mathematical Centre)

Permutation Orbifolds of Vertex Operator Algebras
This is a recording of a talk I gave at the Illinois State University Algebra Seminar. Suggest a problem: https://forms.gle/ea7Pw7HcKePGB4my5 Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.com/stores/michael-penn-math Personal Websi
From playlist Research Talks

Winter School JTP: Introduction to A-infinity structures, Bernhard Keller, Lecture 1
In this minicourse, we will present basic results on A-infinity algebras, their modules and their derived categories. We will start with two motivating problems from representation theory. Then we will briefly present the topological origin of A-infinity structures. We will then define and
From playlist Winter School on “Connections between representation Winter School on “Connections between representation theory and geometry"
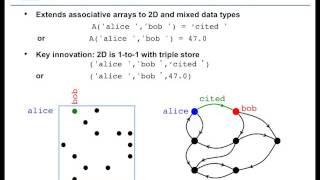
RES.LL-005 D4M: Signal Processing on Databases, Fall 2012 View the complete course: http://ocw.mit.edu/RESLL-005F12 Instructor: Jeremy Kepner Associative array mathematics. Relevant operations on an associative array. Semirings and matrices. See MIT Press book "Mathematics of Big Data."
From playlist MIT D4M: Signal Processing on Databases, Fall 2012

Marcy Robertson: Expansions, completions and automorphisms of welded tangled foams
SMRI Seminar: Marcy Robertson (University of Melbourne) Abstract: Welded tangles are knotted surfaces in R^4. Bar-Natan and Dancso described a class of welded tangles which have "foamed vertices" where one allows surfaces to merge and split. The resulting welded tangled foams carry an alg
From playlist SMRI Seminars

Nijenhuis Geometry Chair's Talk 2 (Alexey Bolsinov)
SMRI -MATRIX Symposium: Nijenhuis Geometry and Integrable Systems Chair's Talk 2 (Alexey Bolsinov) 8 February 2022 ---------------------------------------------------------------------------------------------------------------------- SMRI-MATRIX Joint Symposium, 7 – 18 February 2022 Week
From playlist MATRIX-SMRI Symposium: Nijenhuis Geometry and integrable systems

