
Jacob explains the fundamental concepts in group theory of what groups and subgroups are, and highlights a few examples of groups you may already know. Abelian groups are named in honor of Niels Henrik Abel (https://en.wikipedia.org/wiki/Niels_Henrik_Abel), who pioneered the subject of
From playlist Basics: Group Theory

This lecture is part of an online math course on group theory. We review free abelian groups, then construct free (non-abelian) groups, and show that they are given by the set of reduced words, and as a bonus find that they are residually finite.
From playlist Group theory

Every Group of Order Five or Smaller is Abelian Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Every Group of Order Five or Smaller is Abelian Proof. In this video we prove that if G is a group whose order is five or smaller, then G must be abelian.
From playlist Abstract Algebra

Group theory 17: Finite abelian groups
This lecture is part of a mathematics course on group theory. It shows that every finitely generated abelian group is a sum of cyclic groups. Correction: At 9:22 the generators should be g, h+ng not g, g+nh
From playlist Group theory

Every Subgroup of an Abelian Group is Normal Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Every Subgroup of an Abelian Group is Normal Proof
From playlist Abstract Algebra

Representation theory: Abelian groups
This lecture discusses the complex representations of finite abelian groups. We show that any group is iomorphic to its dual (the group of 1-dimensional representations, and isomorphic to its double dual in a canonical way (Pontryagin duality). We check the orthogonality relations for the
From playlist Representation theory

Before we carry on with our coset journey, we need to discover when the left- and right cosets are equal to each other. The obvious situation is when our group is Abelian. The other situation is when the subgroup is a normal subgroup. In this video I show you what a normal subgroup is a
From playlist Abstract algebra

Visual Group Theory, Lecture 4.4: Finitely generated abelian groups
Visual Group Theory, Lecture 4.4: Finitely generated abelian groups We begin this lecture by proving that the cyclic group of order n*m is isomorphic to the direct product of cyclic groups of order n and m if and only if gcd(n,m)=1. Then, we classify all finite abelian groups by decomposi
From playlist Visual Group Theory
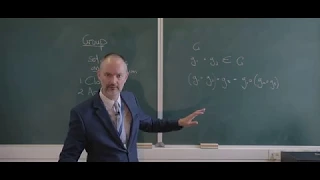
Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

Francesc Fité, Sato-Tate groups of abelian varieties of dimension up to 3
VaNTAGe seminar on April 7, 2020 License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

Visual Group Theory, Lecture 4.5: The isomorphism theorems
Visual Group Theory, Lecture 4.5: The isomorphism theorems There are four central results in group theory that are collectively known at the isomorphism theorems. We introduced the first of these a few lectures back, under the name of the "fundamental homomorphism theorem." In this lectur
From playlist Visual Group Theory

Andrew Wiles: Fermat's Last theorem: abelian and non-abelian approaches
The successful approach to solving Fermat's problem reflects a move in number theory from abelian to non-abelian arithmetic. This lecture was held by Abel Laurate Sir Andrew Wiles at The University of Oslo, May 25, 2016 and was part of the Abel Prize Lectures in connection with the Abel P
From playlist Sir Andrew J. Wiles

Stefano Marseglia, Computing isomorphism classes of abelian varieties over finite fields
VaNTAGe Seminar, February 1, 2022 License: CC-BY-NC-SA Links to some of the papers mentioned in this talk: Honda: https://doi.org/10.2969/jmsj/02010083 Tate: https://link.springer.com/article/10.1007/BF01404549 Deligne: https://eudml.org/doc/141987 Hofmann, Sircana: https://arxiv.org/ab
From playlist Curves and abelian varieties over finite fields

GT22. The Fundamental Theorem of Finite Abelian Groups
Edit for 5:45: Proof of FTFAG needs more steps as follows (thanks to Jack Shotton for the example in the comments): Case 3: First note, if some [xi] does not contain y, then it maps isomorphically to Z/mi in G/H. One can then show that G= [xi] x Gi, where Gi is generated by the other x
From playlist Abstract Algebra

Visual Group Theory, Lecture 2.1: Cyclic and abelian groups
Visual Group Theory, Lecture 2.1: Cyclic and abelian groups In this lecture, we introduce two important families of groups: (1) "cyclic groups", which are those that can be generated by a single element, and (2) "abelian groups", which are those for which multiplication commutes. Addition
From playlist Visual Group Theory

The Structure of the Group of Rational Points of an Abelian Variety (CTNT Online, June 12-14, 2020)
This video was created for the CTNT 2020 Conference (June 12-14, 2020): https://ctnt-summer.math.uconn.edu/ctnt-conference-2020-online/ (Preprint) The Structure of the Group of Rational Points of an Abelian Variety over a Finite Field: https://arxiv.org/abs/2006.00637 My contact informat
From playlist CTNT 2020 - Conference Videos