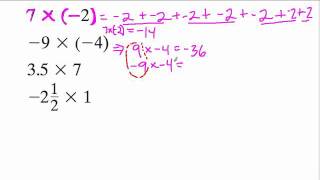Elementary arithmetic | Numbers
Negative number
In mathematics, a negative number represents an opposite. In the real number system, a negative number is a number that is less than zero. Negative numbers are often used to represent the magnitude of a loss or deficiency. A debt that is owed may be thought of as a negative asset. If a quantity, such as the charge on an electron, may have either of two opposite senses, then one may choose to distinguish between those senses—perhaps arbitrarily—as positive and negative. Negative numbers are used to describe values on a scale that goes below zero, such as the Celsius and Fahrenheit scales for temperature. The laws of arithmetic for negative numbers ensure that the common-sense idea of an opposite is reflected in arithmetic. For example, −(−3) = 3 because the opposite of an opposite is the original value. Negative numbers are usually written with a minus sign in front. For example, −3 represents a negative quantity with a magnitude of three, and is pronounced "minus three" or "negative three". To help tell the difference between a subtraction operation and a negative number, occasionally the negative sign is placed slightly higher than the minus sign (as a superscript). Conversely, a number that is greater than zero is called positive; zero is usually (but not always) thought of as neither positive nor negative. The positivity of a number may be emphasized by placing a plus sign before it, e.g. +3. In general, the negativity or positivity of a number is referred to as its sign. Every real number other than zero is either positive or negative. The non-negative whole numbers are referred to as natural numbers (i.e., 0, 1, 2, 3...), while the positive and negative whole numbers (together with zero) are referred to as integers. (Some definitions of the natural numbers exclude zero.) In bookkeeping, amounts owed are often represented by red numbers, or a number in parentheses, as an alternative notation to represent negative numbers. Negative numbers appeared for the first time in history in the Nine Chapters on the Mathematical Art, which in its present form dates from the period of the Chinese Han Dynasty (202 BC – AD 220), but may well contain much older material. Liu Hui (c. 3rd century) established rules for adding and subtracting negative numbers. By the 7th century, Indian mathematicians such as Brahmagupta were describing the use of negative numbers. Islamic mathematicians further developed the rules of subtracting and multiplying negative numbers and solved problems with negative coefficients. Prior to the concept of negative numbers, mathematicians such as Diophantus considered negative solutions to problems "false" and equations requiring negative solutions were described as absurd. Western mathematicians like Leibniz (1646–1716) held that negative numbers were invalid, but still used them in calculations. (Wikipedia).
_mess_tent_still_does_not_break_out_of_the_sub-freezing_temperatures.jpg?width=300)