
Definition of a Field In this video, I define the concept of a field, which is basically any set where you can add, subtract, add, and divide things. Then I show some neat properties that have to be true in fields. Enjoy! What is an Ordered Field: https://youtu.be/6mc5E6x7FMQ Check out
From playlist Real Numbers

All About Closed Sets and Closures of Sets (and Clopen Sets) | Real Analysis
We introduced closed sets and clopen sets. We'll visit two definitions of closed sets. First, a set is closed if it is the complement of some open set, and second, a set is closed if it contains all of its limit points. We see examples of sets both closed and open (called "clopen sets") an
From playlist Real Analysis
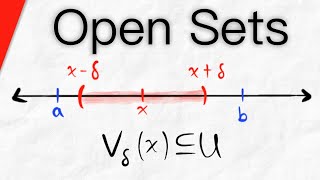
Intro to Open Sets (with Examples) | Real Analysis
We introduce open sets in the context of the real numbers, along with examples and nonexamples of open sets. This is an important topic in the topology of the reals. We say a subset U of the reals is open if, for any x in U, there exists a delta-neighborhood of x that is contained in U. We
From playlist Real Analysis

A Set is Closed iff it Contains Limit Points | Real Analysis
We prove the equivalence of two definitions of closed sets. We may say a set is closed if it is the complement of some open set, or a set is closed if it contains its limit points. These definitions are equivalent, so we'll prove a set is closed if and only if it contains its limit points.
From playlist Real Analysis

Field Theory - Algebraically Closed Fields - Lecture 9
In this video we define what an algebraically closed field and assert without proof that they exist. We also explain why if you can find a single root for any polynomial, then you can find them all.
From playlist Field Theory

Ordered Fields In this video, I define the notion of an order (or inequality) and then define the concept of an ordered field, and use this to give a definition of R using axioms. Actual Construction of R (with cuts): https://youtu.be/ZWRnZhYv0G0 COOL Construction of R (with sequences)
From playlist Real Numbers
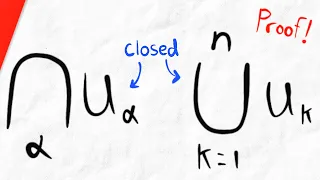
Proof for Unions and Intersections of Closed Sets | Real Analysis
We prove the intersection of an arbitrary collection of closed sets is closed, and the union of a finite collection of closed sets is closed. To do this, we use DeMorgan's Laws, the definition of closed and open sets, and previously proven results on the unions and intersections of open se
From playlist Real Analysis

Limit Points (Sequence and Neighborhood Definition) | Real Analysis
Limit points, accumulation points, cluster points, whatever you call them - that's today's subject. We'll define limit points in two ways. First we'll discuss the sequence definition of a limit point of a set. Then we'll discuss the neighborhood definition of a limit point of a set. We wil
From playlist Real Analysis

Open Covers, Finite Subcovers, and Compact Sets | Real Analysis
We introduce coverings of sets, finite subcovers, and compact sets in the context of real analysis. These concepts will be critical in our continuing discussion of the topology of the reals. The definition of a compact set, in particular, is surprisingly fundamental, and we will provide an
From playlist Real Analysis

Salma Kuhlmann: Real closed fields and models of Peano arithmetic
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist SPECIAL 7th European congress of Mathematics Berlin 2016.

Elliot Kaplan, McMaster Unviersity
October 7, Elliot Kaplan, McMaster Unviersity Generic derivations on o-minimal structures
From playlist Fall 2021 Online Kolchin Seminar in Differential Algebra

Omar Leon Sanchez University of Manchester Differentially large fields Recall that a field K is large if it is existentially closed in the field of Laurent series K((t)). Examples of such fields are the complex, the real, and the p-adic numbers. This class of fields has been exploited si
From playlist Fall 2019 Kolchin Seminar in Differential Algebra

Strongly minimal groups in o-minimal structures - K. Peterzil - Workshop 3 - CEB T1 2018
Kobi Peterzil (Haifa) / 27.03.2018 Strongly minimal groups in o-minimal structures Let G be a definable two-dimensional group in an o-minimal structure M and let D be a strongly minimal expansion of G, whose atomic relations are definable in M. We prove that if D is not locally modular t
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields
Vincent Bagayoko, École Polytechnique
February 26, Vincent Bagayoko, École Polytechnique Three flavors of H-fields
From playlist Spring 2021 Online Kolchin Seminar in Differential Algebra

Erlend Fornæss Wold: Symplectic Carleman approximation on co-adjoint orbits
For a complex Lie group $G$ with a real form $G_{0}\subset G$, we prove that any Hamiltionian automorphism $\phi$ of a coadjoint orbit $\mathcal{O}_{0}$ of $G_{0}$ whose connected components are simply connected, may be approximated by holomorphic $O_{0}$-invariant symplectic automorphism
From playlist Analysis and its Applications

Abraham Robinson’s legacy in model theory and (...) - L. Van den Dries - Workshop 3 - CEB T1 2018
Lou Van den Dries (University of Illinois, Urbana) / 27.03.2018 Abraham Robinson’s legacy in model theory and its applications ---------------------------------- Vous pouvez nous rejoindre sur les réseaux sociaux pour suivre nos actualités. Facebook : https://www.facebook.com/InstitutHe
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

A tour of globally valued fields - E. Hrushovski - Workshop 3 - CEB T1 2018
Ehud Hrushovski (Oxford) / 26.03.2018 A tour of globally valued fields This will be a gentle introduction to the emerging model theory of GVFs, using a number of specific formulas as examples. ---------------------------------- Vous pouvez nous rejoindre sur les réseaux sociaux pour sui
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields
CTNT 2020 - Infinite Galois Theory (by Keith Conrad) - Lecture 3
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Infinite Galois Theory (by Keith Conrad)
Chris Miller: Expansions of the real field by trajectories of definable vector fields
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

An Example of a Closed Continuous Function that is Not Open
An Example of a Closed Continuous Function that is Not Open If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Topology