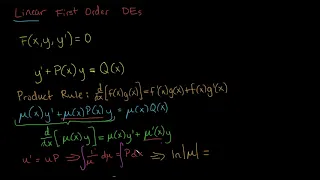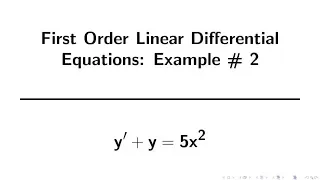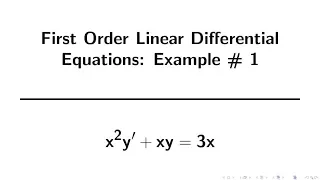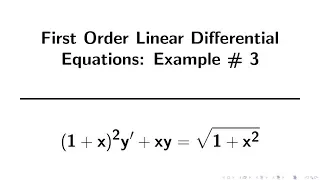Predicate logic | Model theory | Systems of formal logic
First-order logic
First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists" is a quantifier, while x is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic. A theory about a topic is usually a first-order logic together with a specified domain of discourse (over which the quantified variables range), finitely many functions from that domain to itself, finitely many predicates defined on that domain, and a set of axioms believed to hold about them. Sometimes, "theory" is understood in a more formal sense as just a set of sentences in first-order logic. The adjective "first-order" distinguishes first-order logic from higher-order logic, in which there are predicates having predicates or functions as arguments, or in which quantification over predicates or functions, or both, are permitted. In first-order theories, predicates are often associated with sets. In interpreted higher-order theories, predicates may be interpreted as sets of sets. There are many deductive systems for first-order logic which are both sound (i.e., all provable statements are true in all models) and complete (i.e. all statements which are true in all models are provable). Although the logical consequence relation is only semidecidable, much progress has been made in automated theorem proving in first-order logic. First-order logic also satisfies several metalogical theorems that make it amenable to analysis in proof theory, such as the Löwenheim–Skolem theorem and the compactness theorem. First-order logic is the standard for the formalization of mathematics into axioms, and is studied in the foundations of mathematics.Peano arithmetic and Zermelo–Fraenkel set theory are axiomatizations of number theory and set theory, respectively, into first-order logic.No first-order theory, however, has the strength to uniquely describe a structure with an infinite domain, such as the natural numbers or the real line. Axiom systems that do fully describe these two structures (that is, categorical axiom systems) can be obtained in stronger logics such as second-order logic. The foundations of first-order logic were developed independently by Gottlob Frege and Charles Sanders Peirce. For a history of first-order logic and how it came to dominate formal logic, see José Ferreirós (2001). (Wikipedia).