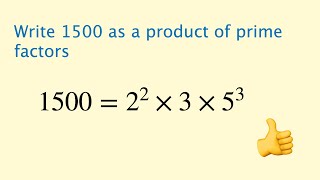Articles containing proofs | Prime numbers | Integer sequences
Prime number
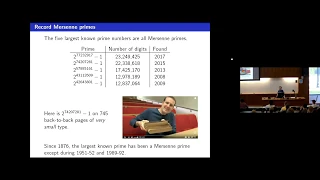
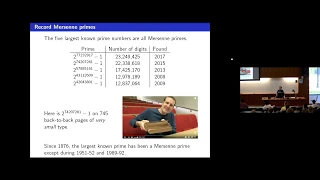
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself.However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always produces the correct answer in polynomial time but is too slow to be practical. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. As of December 2018 the largest known prime number is a Mersenne prime with 24,862,048 decimal digits. There are infinitely many primes, as demonstrated by Euclid around 300 BC. No known simple formula separates prime numbers from composite numbers. However, the distribution of primes within the natural numbers in the large can be statistically modelled. The first result in that direction is the prime number theorem, proven at the end of the 19th century, which says that the probability of a randomly chosen large number being prime is inversely proportional to its number of digits, that is, to its logarithm. Several historical questions regarding prime numbers are still unsolved. These include Goldbach's conjecture, that every even integer greater than 2 can be expressed as the sum of two primes, and the twin prime conjecture, that there are infinitely many pairs of primes having just one even number between them. Such questions spurred the development of various branches of number theory, focusing on analytic or algebraic aspects of numbers. Primes are used in several routines in information technology, such as public-key cryptography, which relies on the difficulty of factoring large numbers into their prime factors. In abstract algebra, objects that behave in a generalized way like prime numbers include prime elements and prime ideals. (Wikipedia).