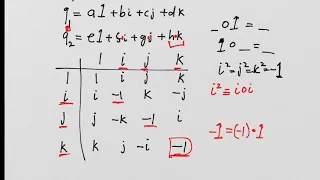Field (mathematics) | Algebraic number theory
Algebraic number field
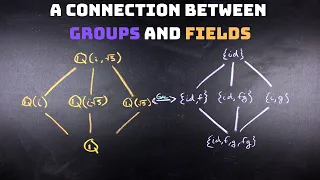
In mathematics, an algebraic number field (or simply number field) is an extension field of the field of rational numbers such that the field extension has finite degree (and hence is an algebraic field extension).Thus is a field that contains and has finite dimension when considered as a vector space over . The study of algebraic number fields, and, more generally, of algebraic extensions of the field of rational numbers, is the central topic of algebraic number theory. This study reveals hidden structures behind usual rational numbers, by using algebraic methods. (Wikipedia).