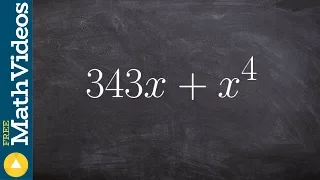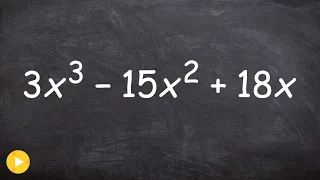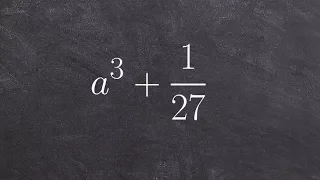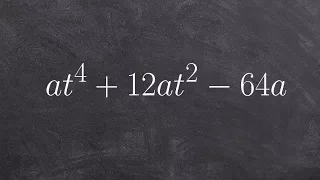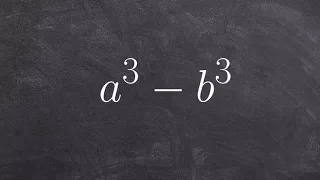Computational hardness assumptions | Integer factorization algorithms | Unsolved problems in computer science | Factorization
Integer factorization
In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these factors are further restricted to prime numbers, the process is called prime factorization. When the numbers are sufficiently large, no efficient non-quantum integer factorization algorithm is known. However, it has not been proven that such an algorithm does not exist. The presumed difficulty of this problem is important for the algorithms used in cryptography such as RSA public-key encryption and the RSA digital signature. Many areas of mathematics and computer science have been brought to bear on the problem, including elliptic curves, algebraic number theory, and quantum computing. In 2019, Fabrice Boudot, Pierrick Gaudry, Aurore Guillevic, Nadia Heninger, Emmanuel Thomé and Paul Zimmermann factored a 240-digit (795-bit) number (RSA-240) utilizing approximately 900 core-years of computing power. The researchers estimated that a 1024-bit RSA modulus would take about 500 times as long. Not all numbers of a given length are equally hard to factor. The hardest instances of these problems (for currently known techniques) are semiprimes, the product of two prime numbers. When they are both large, for instance more than two thousand bits long, randomly chosen, and about the same size (but not too close, for example, to avoid efficient factorization by Fermat's factorization method), even the fastest prime factorization algorithms on the fastest computers can take enough time to make the search impractical; that is, as the number of digits of the primes being factored increases, the number of operations required to perform the factorization on any computer increases drastically. Many cryptographic protocols are based on the difficulty of factoring large composite integers or a related problem—for example, the RSA problem. An algorithm that efficiently factors an arbitrary integer would render RSA-based public-key cryptography insecure. (Wikipedia).