Irreducible polynomial

Abstract algebra | Polynomials | Algebra

In mathematics, an irreducible polynomial is, roughly speaking, a polynomial that cannot be factored into the product of two non-constant polynomials. The property of irreducibility depends on the nature of the coefficients that are accepted for the possible factors, that is, the field to which the coefficients of the polynomial and its possible factors are supposed to belong. For example, the polynomial x2 − 2 is a polynomial with integer coefficients, but, as every integer is also a real number, it is also a polynomial with real coefficients. It is irreducible if it is considered as a polynomial with integer coefficients, but it factors as if it is considered as a polynomial with real coefficients. One says that the polynomial x2 − 2 is irreducible over the integers but not over the reals. Polynomial irreducibility can be considered for polynomials with coefficients in an integral domain, and there are two common definitions. Most often, a polynomial over an integral domain R is said to be irreducible if it is not the product of two polynomials that have their coefficients in R, and are not unit in R. Equivalently, for this definition, an irreducible polynomial is an irreducible element in the rings of polynomials over R. If R is a field, the two definitions of irreducibility are equivalent. For the second definition, a polynomial is irreducible if it cannot be factored into polynomials with coefficients in the same domain that both have a positive degree. Equivalently, a polynomial is irreducible if it is irreducible over the field of fractions of the integral domain. For example, the polynomial is irreducible for the second definition, and not for the first one. On the other hand, is irreducible in for the two definitions, while it is reducible in A polynomial that is irreducible over any field containing the coefficients is absolutely irreducible. By the fundamental theorem of algebra, a univariate polynomial is absolutely irreducible if and only if its degree is one. On the other hand, with several indeterminates, there are absolutely irreducible polynomials of any degree, such as for any positive integer n. A polynomial that is not irreducible is sometimes said to be a reducible polynomial. Irreducible polynomials appear naturally in the study of polynomial factorization and algebraic field extensions. It is helpful to compare irreducible polynomials to prime numbers: prime numbers (together with the corresponding negative numbers of equal magnitude) are the irreducible integers. They exhibit many of the general properties of the concept of "irreducibility" that equally apply to irreducible polynomials, such as the essentially unique factorization into prime or irreducible factors. When the coefficient ring is a field or other unique factorization domain, an irreducible polynomial is also called a prime polynomial, because it generates a prime ideal. (Wikipedia).

Irreducible Polynomials

In this video I discuss irreducible polynomials and tests for irreducibility. Note that this video is intended for students in abstract algebra and is not appropriate for high-school or early college level algebra courses.

From playlist Abstract Algebra

Abstract Algebra | Irreducible polynomials

We introduce the notion of an irreducible polynomial over the ring k[x] where k is any field. A proof that p(x) is irreducible if and only if (p(x)) is maximal is also given, along with some examples. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal W

From playlist Abstract Algebra

Alina Ostafe: Dynamical irreducibility of polynomials modulo primes

Abstract: In this talk we look at polynomials having the property that all compositional iterates are irreducible, which we call dynamical irreducible. After surveying some previous results (mostly over finite fields), we will concentrate on the question of the dynamical irreducibility of

From playlist Number Theory Down Under 9

Irreducibility (Eisenstein's Irreducibility Criterion)

Given a polynomial with integer coefficients, we can determine whether it's irreducible over the rationals using Eisenstein's Irreducibility Criterion. Unlike some our other technique, this works for polynomials of high degree! The tradeoff is that it works over the rationals, but need not

From playlist Modern Algebra - Chapter 11

Field Theory: Irreducible Polynomials

This video is about irreducible polynomials.

From playlist Basics: Field Theory

Visual Group Theory, Lecture 6.3: Polynomials and irreducibility

Visual Group Theory, Lecture 6.3: Polynomials and irreducibility A complex number is algebraic over Q (the rationals) if it is the root of a polynomial with rational coefficients. It is clear that every number that can be written with arithmetic and radicals is rational. Galois' big achie

From playlist Visual Group Theory

Abstract Algebra | Irreducibles and Primes in Integral Domains

We define the notion of an irreducible element and a prime element in the context of an arbitrary integral domain. Further, we give examples of irreducible elements that are not prime. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://

From playlist Abstract Algebra

FIT3.1.4. Factoring Example: Artin-Schreier Polynomials

Field Theory: We show that g(x)=x^5-x+1 is irreducible over the rationals using techniques from finite fields. This leads to the definition of an Artin-Schreier polynomial, and in turn we obtain a class of irreducible polynomials over the rationals and prime characteristic.

From playlist Abstract Algebra

FIT3.1.1. Roots of Polynomials

Field Theory: We recall basic factoring results for polynomials from Ring Theory and give a definition of a splitting field. This allows one to consider any irreducible polynomial as a set of roots, and in turn we consider when an irreducible polynomial can have multiple roots. We finish

From playlist Abstract Algebra

Rings 16 Factorization of polynomials

This lecture is part of an online course on rings and modules. We discuss the problem of factorising polynomials with integer coefficients, and in particular give some tests to see whether they are irreducible. For the other lectures in the course see https://www.youtube.com/playlist?lis

From playlist Rings and modules

Lecture 12. UFD[x] is UFD. Factoring integer polynomials

From playlist Abstract Algebra 2

Galois theory: Finite fields

This lecture is part of an online graduate course on Galois theory. We use the theory of splitting fields to classify finite fields: there is one of each prime power order (up to isomorphism). We give a few examples of small order, and point out that there seems to be no good choice for

From playlist Galois theory

Factors of sparse polynomials: structural results and some algorithms - Shubhangi Saraf

Computer Science/Discrete Mathematics Seminar II Topic: Factors of sparse polynomials: structural results and some algorithms Speaker: Shubhangi Saraf Affiliation: Member, School of Mathematics Date: March 26, 2019 For more video please visit http://video.ias.edu

From playlist Mathematics

Lecture 32. Adjoining roots and splitting fields

From playlist Abstract Algebra 2

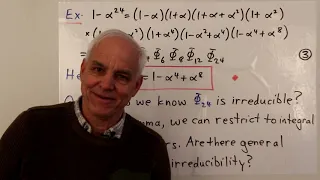
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger

In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some

From playlist Famous Math Problems

Irreducible polynomial

Related pages