
From playlist Songs to Torture Undergrads

Some comments on the notation used in Calculus, and how the notation relates to a function that it represents.
From playlist Calculus Chapter 5 (selected videos)

Yes. I make mistakes ... rarely. http://www.flippingphysics.com
From playlist Miscellaneous

Narcissism is the word we routinely use to describe someone self-satisfied and arrogant. But what do we really mean by the word – and are we applying it correctly? If you like our films, take a look at our shop (we ship worldwide): https://goo.gl/YfXSQO Join our mailing list: http://bit.ly
From playlist SELF

In this video, you’ll learn more about the strategies you can use to avoid plagiarizing others' work. Visit https://edu.gcfglobal.org/en/useinformationcorrectly/avoiding-plagiarism/1/ for our text-based lesson. We hope you enjoy!
From playlist Job Success

YouTube Has Blacklisted My Channel
YouTube is refusing to suggest my content to my subscribers and wider audiences. This can't go on. If you value my videos, please support my independent work on: https://www.patreon.com/thehatedone I have never trusted YouTube. I have always considered it a necessary evil for this channe
From playlist All of my videos

Why do I keep trying to use music?
Oh yes, because I need the practice... #BathSinging
From playlist Nerdy Rodent Uploads!
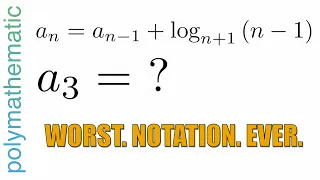
A Most Unfair Test Question: Combining Sequence Notation and Log Notation in the Same Problem
If you ever wanted to know how to trigger a mathematician, this would be the way to do it. This is the worst misuse of mathematical notation I've ever seen. It combines sequence notation (subscripts that don't typically have operational value) with logarithmic base notation (subscripts tha
From playlist Math Mini

[Lesson 3] QED Prerequisites Dirac Formalism Part 3
This lesson is about the Dirac formalism's approach to linear operators. These operators will be the core of the theory of quantum mechanics, and the Dirac formalism is a very tight way of understanding them. [reposted to fix small error in title screen] Please consider supporting this c
From playlist QED- Prerequisite Topics
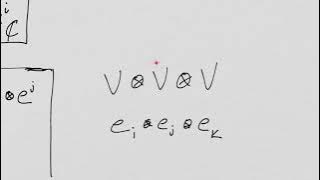
[Lesson 11] QED Prerequisites - Tensor Product Spaces
We take a detour from the Angular Momentum Mind Map to cover the important topic of Tensor Product spaces in the Dirac Formalism. In quantum mechanics, the notion of tensors is hidden under the hood of the formalism and this lesson opens that hood. The goal is to make us confident that we
From playlist QED- Prerequisite Topics

Integral of absolute value of x (abs x)
In this video we're finding the Integral of absolute value of x (abs x). Enjoy! Some of the links below are affiliate links. As an Amazon Associate I earn from qualifying purchases. If you purchase through these links, it won't cost you any additional cash, but it will help to support m
From playlist Integrals, Integrals, Integrals

Vincent Vargas - 1/4 Liouville conformal field theory and the DOZZ formula
Materials: http://marsweb.ihes.fr/Cours_Vargas.pdf Liouville conformal field theory (LCFT hereafter), introduced by Polyakov in his 1981 seminal work "Quantum geometry of bosonic strings", can be seen as a random version of the theory of Riemann surfaces. LCFT appears in Polyakov's work a
From playlist Vincent Vargas - Liouville conformal field theory and the DOZZ formula
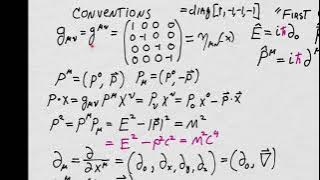
QED Prerequisites: Field Equations - Conventions
In this lesson we lay down the notation conventions used for our introduction to the two key field equations used in elementary QED: the Klein-Gordon Equation and the Dirac Equation. These subjects are often taught at the beginning of a QED course, but we will treat them as pre-requisite c
From playlist QED- Prerequisite Topics

Greg Fasshauer: Some recent insights into computing with positive definite kernels
Abstract: In this talk I will discuss recent joint work with Mike McCourt (SigOpt, San Francisco) that has led to progress on the numerically stable computation of certain quantities of interest when working with positive definite kernels to solve scattered data interpolation (or kriging)
From playlist Numerical Analysis and Scientific Computing

Vincent Vargas - 3/4 Liouville conformal field theory and the DOZZ formula
Materials: http://marsweb.ihes.fr/Cours_Vargas.pdf Liouville conformal field theory (LCFT hereafter), introduced by Polyakov in his 1981 seminal work "Quantum geometry of bosonic strings", can be seen as a random version of the theory of Riemann surfaces. LCFT appears in Polyakov's work a
From playlist Vincent Vargas - Liouville conformal field theory and the DOZZ formula

Metric Spaces - Lectures 15 & 16: Oxford Mathematics 2nd Year Student Lecture
For the first time we are making a full Oxford Mathematics Undergraduate lecture course available. Ben Green's 2nd Year Metric Spaces course is the first half of the Metric Spaces and Complex Analysis course. This is the 8th of 11 videos. The course is about the notion of distance. You ma
From playlist Oxford Mathematics Student Lectures - Metric Spaces

Excel Song - we all work with excel spreadsheets
I don't post on YouTube much anymore, follow me on Instagram instead! @karenxcheng
From playlist Excel Songs

Applications of the theory of the ̄∂ equation (Lecture 2) by Vamsi Pingali
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019
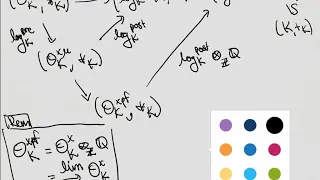
The p-Adic Logarithm - Part 05 - (Toy) Log Links
We are now going to define log-linked fields. This originates in AAG3 but not phrased exactly in this way. Hopefully this presentation simplifies things.
From playlist p-adic log
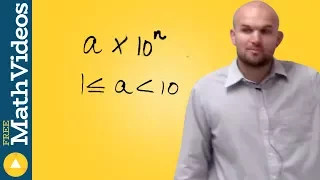
What is the definition of scientific notation
👉 Learn about scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is the number of digits up to t
From playlist Scientific Notation | Learn About