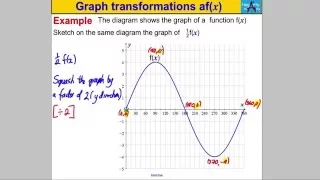
Affine geometry | Transformation (function)
Affine transformation
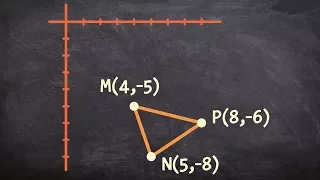
In Euclidean geometry, an affine transformation or affinity (from the Latin, affinis, "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles. More generally, an affine transformation is an automorphism of an affine space (Euclidean spaces are specific affine spaces), that is, a function which maps an affine space onto itself while preserving both the dimension of any affine subspaces (meaning that it sends points to points, lines to lines, planes to planes, and so on) and the ratios of the lengths of parallel line segments. Consequently, sets of parallel affine subspaces remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. If X is the point set of an affine space, then every affine transformation on X can be represented as the composition of a linear transformation on X and a translation of X. Unlike a purely linear transformation, an affine transformation need not preserve the origin of the affine space. Thus, every linear transformation is affine, but not every affine transformation is linear. Examples of affine transformations include translation, scaling, homothety, similarity, reflection, rotation, shear mapping, and compositions of them in any combination and sequence. Viewing an affine space as the complement of a hyperplane at infinity of a projective space, the affine transformations are the projective transformations of that projective space that leave the hyperplane at infinity invariant, restricted to the complement of that hyperplane. A generalization of an affine transformation is an affine map (or affine homomorphism or affine mapping) between two (potentially different) affine spaces over the same field k. Let (X, V, k) and (Z, W, k) be two affine spaces with X and Z the point sets and V and W the respective associated vector spaces over the field k. A map f: X → Z is an affine map if there exists a linear map mf : V → W such that mf (x − y) = f (x) − f (y) for all x, y in X. (Wikipedia).