Abstract algebra | Lie groups | Linear algebra | Linear algebraic groups
General linear group
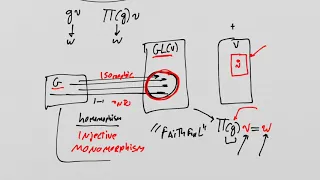
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible, with identity matrix as the identity element of the group. The group is so named because the columns (and also the rows) of an invertible matrix are linearly independent, hence the vectors/points they define are in general linear position, and matrices in the general linear group take points in general linear position to points in general linear position. To be more precise, it is necessary to specify what kind of objects may appear in the entries of the matrix. For example, the general linear group over R (the set of real numbers) is the group of n×n invertible matrices of real numbers, and is denoted by GLn(R) or GL(n, R). More generally, the general linear group of degree n over any field F (such as the complex numbers), or a ring R (such as the ring of integers), is the set of n×n invertible matrices with entries from F (or R), again with matrix multiplication as the group operation. Typical notation is GLn(F) or GL(n, F), or simply GL(n) if the field is understood. More generally still, the GL(V) is the abstract automorphism group, not necessarily written as matrices. The , written SL(n, F) or SLn(F), is the subgroup of GL(n, F) consisting of matrices with a determinant of 1. The group GL(n, F) and its subgroups are often called linear groups or matrix groups (the abstract group GL(V) is a linear group but not a matrix group). These groups are important in the theory of group representations, and also arise in the study of spatial symmetries and symmetries of vector spaces in general, as well as the study of polynomials. The modular group may be realised as a quotient of the special linear group SL(2, Z). If n ≥ 2, then the group GL(n, F) is not abelian. (Wikipedia).