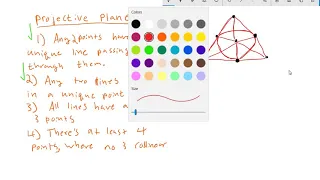
Projective space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines. This definition of a projective space has the disadvantage of not being isotropic, having two different sorts of points, which must be considered separately in proofs. Therefore, other definitions are generally preferred. There are two classes of definitions. In synthetic geometry, point and line are primitive entities that are related by the incidence relation "a point is on a line" or "a line passes through a point", which is subject to the axioms of projective geometry. For some such set of axioms, the projective spaces that are defined have been shown to be equivalent to those resulting from the following definition, which is more often encountered in modern textbooks. Using linear algebra, a projective space of dimension n is defined as the set of the vector lines (that is, vector subspaces of dimension one) in a vector space V of dimension n + 1. Equivalently, it is the quotient set of V \ {0} by the equivalence relation "being on the same vector line". As a vector line intersects the unit sphere of V in two antipodal points, projective spaces can be equivalently defined as spheres in which antipodal points are identified. A projective space of dimension 1 is a projective line, and a projective space of dimension 2 is a projective plane. Projective spaces are widely used in geometry, as allowing simpler statements and simpler proofs. For example, in affine geometry, two distinct lines in a plane intersect in at most one point, while, in projective geometry, they intersect in exactly one point. Also, there is only one class of conic sections, which can be distinguished only by their intersections with the line at infinity: two intersection points for hyperbolas; one for the parabola, which is tangent to the line at infinity; and no real intersection point of ellipses. In topology, and more specifically in manifold theory, projective spaces play a fundamental role, being typical examples of non-orientable manifolds. (Wikipedia).