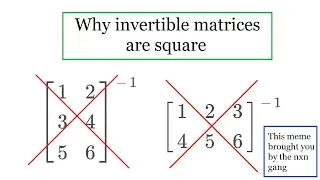
Invertible matrix

Determinants | Matrix theory | Linear algebra | Matrices

In linear algebra, an n-by-n square matrix A is called invertible (also nonsingular or nondegenerate), if there exists an n-by-n square matrix B such that where In denotes the n-by-n identity matrix and the multiplication used is ordinary matrix multiplication. If this is the case, then the matrix B is uniquely determined by A, and is called the (multiplicative) inverse of A, denoted by A−1. Matrix inversion is the process of finding the matrix B that satisfies the prior equation for a given invertible matrix A. A square matrix that is not invertible is called singular or degenerate. A square matrix is singular if and only if its determinant is zero. Singular matrices are rare in the sense that if a square matrix's entries are randomly selected from any finite region on the number line or complex plane, the probability that the matrix is singular is 0, that is, it will "almost never" be singular. Non-square matrices (m-by-n matrices for which m ≠ n) do not have an inverse. However, in some cases such a matrix may have a left inverse or right inverse. If A is m-by-n and the rank of A is equal to n (n ≤ m), then A has a left inverse, an n-by-m matrix B such that BA = In. If A has rank m (m ≤ n), then it has a right inverse, an n-by-m matrix B such that AB = Im. While the most common case is that of matrices over the real or complex numbers, all these definitions can be given for matrices over any ring. However, in the case of the ring being commutative, the condition for a square matrix to be invertible is that its determinant is invertible in the ring, which in general is a stricter requirement than being nonzero. For a noncommutative ring, the usual determinant is not defined. The conditions for existence of left-inverse or right-inverse are more complicated, since a notion of rank does not exist over rings. The set of n × n invertible matrices together with the operation of matrix multiplication (and entries from ring R) form a group, the general linear group of degree n, denoted GLn(R). (Wikipedia).

Invertible matrices are square

Why invertible matrices must be square. Definition of invertible matrix and showing that a 3x2 and a 2x3 matrix cannot be square. Check out my Matrix Algebra playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmAIZGo2l8SWvsHeeCLzamx0 Subscribe to my channel: https://www.youtube.c

From playlist Matrix Algebra

MATH2018 Lecture 6.2 Special Matrices

We look at the properties of invertible matrices, symmetric matrices, and orthogonal matrices, and discuss some important relationships between them.

From playlist MATH2018 Engineering Mathematics 2D

41 - Determining invertibility and finding the inverse

Algebra 1M - international Course no. 104016 Dr. Aviv Censor Technion - International school of engineering

From playlist Algebra 1M

Invertible Matrices correspond with Invertible Transformations **proof**

Invertible Matrices are an algebraic concept that helps us solve Linear Systems of Equations. Invertible Transformations are a geometric concept where we can "undo" a transformation. But in fact they coincide! In this video, we prove that if you have an invertible matrix, the transformatio

From playlist Linear Algebra (Full Course)

Inverse matrices | Lecture 6 | Matrix Algebra for Engineers

Definition of an inverse matrix. Computation of the inverse of a two-by-two matrix. Join me on Coursera: https://www.coursera.org/learn/matrix-algebra-engineers Lecture notes at http://www.math.ust.hk/~machas/matrix-algebra-for-engineers.pdf Subscribe to my channel: http://www.youtube

From playlist Matrix Algebra for Engineers

Invertible matrix

Checking if a matrix is invertible using row-reduction, without finding A-1 Subscribe to my channel: https://www.youtube.com/channel/UCoOjTxz-u5zU0W38zMkQIFw Check out my Matrix Algebra playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmAIZGo2l8SWvsHeeCLzamx0

From playlist Matrix Algebra

Linear Algebra 2.3.1 Characterizations of Invertible Matrices

From playlist Linear Algebra (Entire Course)

Abstract Algebra | Injective Functions

We give the definition of an injective function, an outline of proving that a given function is injective, and a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/

From playlist Abstract Algebra

Invertible Transformations

Description: Corresponding to our algebraic notion of invertibility, we want a geometric notion. Invertible transformations are defined, and then proven to be equivalent (thank goodness!) to invertible matrices when linear. Learning Objectives: 1) Define an invertible transformation 2) D

From playlist Older Linear Algebra Videos

Tut2 Q1-5 (zoom-recorded tutorial)

online video recording zoom (Tut2, Q 1-5) Q1: 0:0 .. 7:25 Q2: 7:25 .. 16:15 Q3: 16:16 .. 32:20 Q4: 32:48 .. 52:30 Q5: 52:40 .. 1:05:30

From playlist Tutorial 2

40 - Invertible matrices

Algebra 1M - international Course no. 104016 Dr. Aviv Censor Technion - International school of engineering

From playlist Algebra 1M

Math 060 Linear Algebra 03 091214: Elementary Matrices

From playlist Course 4: Linear Algebra

Math 060 091317 Elementary matrices

Recall: definition of elementary matrices. Definition: row equivalence. Row equivalence is an equivalence relation. Various characterizations of invertibility. Procedure to calculate an inverse.

From playlist Course 4: Linear Algebra (Fall 2017)

Lec 1 | MIT 18.085 Computational Science and Engineering I, Fall 2008

Lecture 1: Four special matrices License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu

From playlist MIT 18.085 Computational Science & Engineering I, Fall 2008

Stanford ENGR108: Introduction to Applied Linear Algebra | 2020 | Lecture 30-VMLS left & right inv.

Professor Stephen Boyd Samsung Professor in the School of Engineering Director of the Information Systems Laboratory To follow along with the course schedule and syllabus, visit: https://web.stanford.edu/class/engr108/ To view all online courses and programs offered by Stanford, visit:

From playlist Stanford ENGR108: Introduction to Applied Linear Algebra —Vectors, Matrices, and Least Squares

Tut2 Q1-5, recorded 3Sep2021

Recorded on 3rd Sep 2021 T2,Q1: 0:30-10:09 T2,Q2: 10:20-18:02 T2,Q3: 18:10-24:05 T2,Q4a: 24:20-33:55 T2,Q4b: 34:10-40:22 T2,Q5a: 40:30-44:10 T2,Q5b: 44:20-end

From playlist Tutorial 2

Inverse Matrix

In this neat video, I’m connecting two unexpected worlds of linear algebra. Namely, I show that if T is a linear transformation with matrix A, then the matrix of T^-1 (the inverse transformation) is simply A^-1 (the inverse of a matrix). The proof itself is simply gorgeous and uses a combi

From playlist Linear Transformations

Math 060 091117 Multiplicative Inverses, Elementary Matrices

Multiplicative inverses: definition, examples, uniqueness of. Inverse of a product. Exercise. Invertible matrices and the solution set of a linear system. Elementary row operations correspond to elementary matrices.

From playlist Course 4: Linear Algebra (Fall 2017)

Ex: Determine if a 2x2 Matrix is Invertible (nonsingular) Using a Determinant

This video explains how to use a determinant to determine if a 2x2 matrix is invertible. http://mathispower4u.com

From playlist The Determinant of a Matrix

Invertible matrix

Related pages