Differentiable manifold
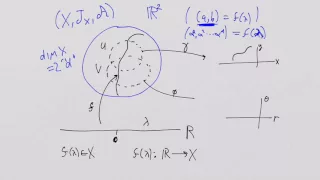
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a vector space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, their compositions on chart intersections in the atlas must be differentiable functions on the corresponding vector space. In other words, where the domains of charts overlap, the coordinates defined by each chart are required to be differentiable with respect to the coordinates defined by every chart in the atlas. The maps that relate the coordinates defined by the various charts to one another are called transition maps. The ability to define such a local differential structure on an abstract space allows one to extend the definition of differentiability to spaces without global coordinate systems. A locally differential structure allows one to define the globally differentiable tangent space, differentiable functions, and differentiable tensor and vector fields. Differentiable manifolds are very important in physics. Special kinds of differentiable manifolds form the basis for physical theories such as classical mechanics, general relativity, and Yang–Mills theory. It is possible to develop a calculus for differentiable manifolds. This leads to such mathematical machinery as the exterior calculus. The study of calculus on differentiable manifolds is known as differential geometry. "Differentiability" of a manifold has been given several meanings, including: continuously differentiable, k-times differentiable, smooth (which itself has many meanings), and analytic. (Wikipedia).