Vector calculus | Differential topology
Vector field
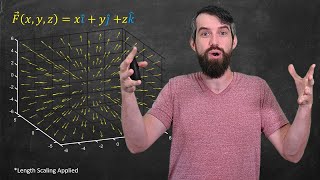
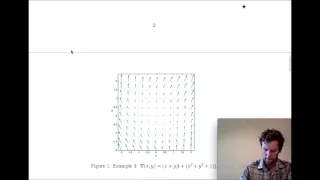
In vector calculus and physics, a vector field is an assignment of a vector to each point in a subset of space. For instance, a vector field in the plane can be visualised as a collection of arrows with a given magnitude and direction, each attached to a point in the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout space, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point. The elements of differential and integral calculus extend naturally to vector fields. When a vector field represents force, the line integral of a vector field represents the work done by a force moving along a path, and under this interpretation conservation of energy is exhibited as a special case of the fundamental theorem of calculus. Vector fields can usefully be thought of as representing the velocity of a moving flow in space, and this physical intuition leads to notions such as the divergence (which represents the rate of change of volume of a flow) and curl (which represents the rotation of a flow). In coordinates, a vector field on a domain in n-dimensional Euclidean space can be represented as a vector-valued function that associates an n-tuple of real numbers to each point of the domain. This representation of a vector field depends on the coordinate system, and there is a well-defined transformation law in passing from one coordinate system to the other. Vector fields are often discussed on open subsets of Euclidean space, but also make sense on other subsets such as surfaces, where they associate an arrow tangent to the surface at each point (a tangent vector). More generally, vector fields are defined on differentiable manifolds, which are spaces that look like Euclidean space on small scales, but may have more complicated structure on larger scales. In this setting, a vector field gives a tangent vector at each point of the manifold (that is, a section of the tangent bundle to the manifold). Vector fields are one kind of tensor field. (Wikipedia).