
Prove the Form of the General Solution to a Linear Second Order Nonhomogeneous DE
This video explains the form of the general solution to linear second order nonhomogeneous differential equations. Site: http://mathispower4u.com
From playlist Linear Second Order Nonhomogeneous Differential Equations: Method of Undetermined Coefficients

The Difference Between an Expression and an Equation
This video explains the difference between an expression and an equation. Site: http://mathispower4u.com Blog: http://mathispower4u.wordpress.com
From playlist Introduction to Linear Equations in One Variable
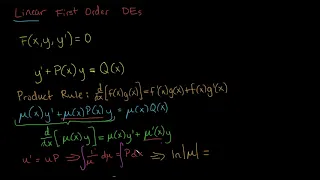
Differential Equations: Linear First Order DEs Introduction
The second of the three analytic methods for solving first order differential equations is only valid if the differential equation is linear. In this video, we look at what it means for a differential equation to be linear and how it can then be solved.
From playlist Differential Equations

The Definition of a Linear Equation in Two Variables
This video defines a linear equation in to variables and provides examples of the different forms of linear equations. http://mathispower4u.com
From playlist The Coordinate Plane, Plotting Points, and Solutions to Linear Equations in Two Variables

Differential Equations | First Order Linear System of DEs.
We solve a nonhomogeneous system of first order linear differential equations using a strategy inspired from solving a single first order linear differential equation. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Systems of Differential Equations

Definition Check: One-to-One and Onto Functions
This video reinforces the definitions of one-to-one functions and onto functions.
From playlist One-to-One and Onto Transformations

Introduction to One-to-One Transformations
This video introduces the topic of one to one transformations.
From playlist One-to-One and Onto Transformations

TAUTOLOGIES, CONTRADICTIONS, and CONTINGENT WFFS - Logic
In this video on #Logic / #PhilosophicalLogic, we learn about tautologies (wffs which are always true), contradictions (wffs which are always false), and contingent wffs (wffs which are both true and false depending on the situation). Then we do some practice exercises. 0:00 [Intro] 0:16
From playlist Logic in Philosophy and Mathematics

Differential Equations: Exact DEs Example 1
It's important to be able to classify a differential equation so we can pick the right method to solve it. In this video, I run through the steps of how to classify a first order differential equation as separable, linear, exact, or neither.
From playlist Differential Equations

How to use PARTIAL TRUTH TABLES to find tautologies, contradictions, and valid arguments - Logic
In this video on #Logic / #PhilosophicalLogic we use partial truth tables to determine whether a wff is a tautology or contradiction. In turn, we use this method to determine whether arguments are valid. This is a much more efficient way than drawing entire truth tables. 0:00 [Intro] 0:3
From playlist Logic in Philosophy and Mathematics
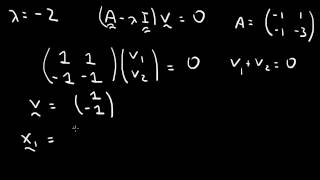
System of linear equations: one eigenvector
Illustrates the solution of a system of two linear, homogeneus equations with one real eigenvalue and one eigenvector. Free books: http://bookboon.com/en/differential-equations-with-youtube-examples-ebook http://www.math.ust.hk/~machas/differential-equations.pdf
From playlist Differential Equations with YouTube Examples

Basic Methods: We define tautology and contradiction and consider the conditions of logical equivalence and implication. Examples include DeMorgan's Laws for logic, modus ponens, and the Law of the Excluded Middle. As a final note, we introduce the Substitution Rules.
From playlist Math Major Basics

Andrei Negut: Hilbert schemes of K3 surfaces
Abstract: We give a geometric representation theory proof of a mild version of the Beauville-Voisin Conjecture for Hilbert schemes of K3 surfaces, namely the injectivity of the cycle map restricted to the subring of Chow generated by tautological classes. Although other geometric proofs o
From playlist Algebraic and Complex Geometry

What are the basics of mathematical logic? | Intro to Math Structures VS1.1
So you want to prove things? Where do you start if you haven't ever written a proof before? In most cases, a course on discrete mathematics or mathematical structures is where someone writes their first proof and that starts with propositional calculus. In this video section, we go through
From playlist The CHALKboard 2022

Show that p V ~p is a Tautology by using a Truth Table
Show that p V ~p is a Tautology by using a Truth Table If you enjoyed this video please consider liking, sharing, and subscribing. Udemy Courses Via My Website: https://mathsorcerer.com My FaceBook Page: https://www.facebook.com/themathsorcerer There are several ways that you can help
From playlist Logical Form and Logical Equivalence

3 Ways to Show a Logical Equivalence | Ex: DeMorgan's Laws
DeMorgan's Laws are two important logical equivalences. In introducing these laws, I talk about three different ways by which you can demonstrate a logical equivalences: There are truth tables, citing known laws, and testing for reasonableness. *******************************************
From playlist Discrete Math (Full Course: Sets, Logic, Proofs, Probability, Graph Theory, etc)

Differential Equation - Introduction (1 of 16) What is a Differential Equation?
Visit http://ilectureonline.com for more math and science lectures! In this video I will define and give examples of what is a differential equation. Next video in the Introduction series can be seen at: http://youtu.be/5mHKirsbdgY
From playlist THE "WHAT IS" PLAYLIST

Noah Arbesfeld: A geometric R-matrix for the Hilbert scheme of points on a general surface
Abstract: We explain how to use a Virasoro algebra to construct a solution to the Yang-Baxter equation acting in the tensor square of the cohomology of the Hilbert scheme of points on a generalsurface S. In the special case where the surface S is C2, the construction appears in work of Mau
From playlist Algebraic and Complex Geometry

