
Manifolds 1.3 : More Examples (Animation Included)
In this video, I introduce the manifolds of product manifolds, tori/the torus, real vectorspaces, matrices, and linear map spaces. This video uses a math animation for visualization. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : http://docdro.id/5koj5
From playlist Manifolds
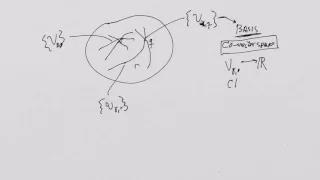
What is a Manifold? Lesson 10: Tangent Space - Basis Vectors
What is a Manifold? Lesson 10: Tangent Space - Basis Vectors
From playlist What is a Manifold?

What is a Manifold? Lesson 6: Topological Manifolds
Topological manifolds! Finally! I had two false starts with this lesson, but now it is fine, I think.
From playlist What is a Manifold?

Manifolds 1.2 : Examples of Manifolds
In this video, I describe basic examples of manifolds. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : http://docdro.id/IZO0G25
From playlist Manifolds

Manifolds 1.1 : Basic Definitions
In this video, I give the basic intuition and definitions of manifolds. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Manifolds

What is a Manifold? Lesson 2: Elementary Definitions
This lesson covers the basic definitions used in topology to describe subsets of topological spaces.
From playlist What is a Manifold?

What is a Manifold? Lesson 14: Quotient Spaces
I AM GOING TO REDO THIS VIDEO. I have made some annotations here and annotations are not visible on mobile devices. STAY TUNED. This is a long lesson about an important topological concept: quotient spaces.
From playlist What is a Manifold?

Transversality and super-rigidity in Gromov-Witten Theory (Lecture – 02) by Chris Wendl
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Chris WENDL - 2/3 Classical transversality methods in SFT
In this talk I will discuss two transversality results that are standard but perhaps not so widely understood: (1) Dragnev's theorem that somewhere injective curves in symplectizations are regular for generic translation-invariant J, and (2) my theorem on automatic transversality in 4-dime
From playlist 2015 Summer School on Moduli Problems in Symplectic Geometry

Christina Sormani: A Course on Intrinsic Flat Convergence part 3
The lecture was held within the framework of the Hausdorff Trimester Program: Optimal Transportation and the Workshop: Winter School & Workshop: New developments in Optimal Transport, Geometry and Analysis
From playlist HIM Lectures 2015

Global existence and convergence of solutions to gradient systems and applications... - Feehan
Analysis Seminar Topic:Global existence and convergence of solutions to gradient systems and applications to Yang-Mills flow Speaker: Paul Feehan Date: Wednesday, February 24 We discuss our results on global existence and convergence of solutions to the gradient flow equation for the Yang
From playlist Mathematics

Transversality and super-rigidity in Gromov-Witten Theory by Chris Wendl
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Manifolds #5: Tangent Space (part 1)
Today, we introduce the notion of tangent vectors and the tangent vector space at a point on a manifold.
From playlist Manifolds

Rigidity for Anosov higher rank lattice actions by Federico Rodriguez-Hertz
PROGRAM SMOOTH AND HOMOGENEOUS DYNAMICS ORGANIZERS: Anish Ghosh, Stefano Luzzatto and Marcelo Viana DATE: 23 September 2019 to 04 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Ergodic theory has its origins in the the work of L. Boltzmann on the kinetic theory of gases.
From playlist Smooth And Homogeneous Dynamics

Viviane Baladi: Transfer operators for Sinai billiards - lecture 1
We will discuss an approach to the statistical properties of two-dimensional dispersive billiards (mostly discrete-time) using transfer operators acting on anisotropic Banach spaces of distributions. The focus of this part will be our recent work with Mark Demers on the measure of maximal
From playlist Analysis and its Applications

Transversality and super-rigidity in Gromov-Witten Theory (Lecture - 04) by Chris Wendl
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Viviane Baladi: Transfer operators for Sinai billiards - lecture 3
We will discuss an approach to the statistical properties of two-dimensional dispersive billiards (mostly discrete-time) using transfer operators acting on anisotropic Banach spaces of distributions. The focus of this part will be our recent work with Mark Demers on the measure of maximal
From playlist Analysis and its Applications

The mother of all representer theorems for inverse problems & machine learning - Michael Unser
This workshop - organised under the auspices of the Isaac Newton Institute on “Approximation, sampling and compression in data science” — brings together leading researchers in the general fields of mathematics, statistics, computer science and engineering. About the event The workshop ai
From playlist Mathematics of data: Structured representations for sensing, approximation and learning

Today, we begin the manifolds series by introducing the idea of a topological manifold, a special type of topological space which is locally homeomorphic to Euclidean space.
From playlist Manifolds
