
MATH331: Riemann Surfaces - part 1
We define what a Riemann Surface is. We show that PP^1 is a Riemann surface an then interpret our crazy looking conditions from a previous video about "holomorphicity at infinity" as coming from the definition of a Riemann Surface.
From playlist The Riemann Sphere
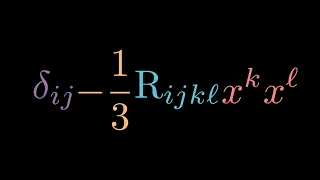
Curvature of a Riemannian Manifold | Riemannian Geometry
In this lecture, we define the exponential mapping, the Riemannian curvature tensor, Ricci curvature tensor, and scalar curvature. The focus is on an intuitive explanation of the curvature tensors. The curvature tensor of a Riemannian metric is a very large stumbling block for many student
From playlist All Videos

Riemannian Geometry - Definition: Oxford Mathematics 4th Year Student Lecture
Riemannian Geometry is the study of curved spaces. It is a powerful tool for taking local information to deduce global results, with applications across diverse areas including topology, group theory, analysis, general relativity and string theory. In these two introductory lectures
From playlist Oxford Mathematics Student Lectures - Riemannian Geometry

Riemannian Geometry - Examples, pullback: Oxford Mathematics 4th Year Student Lecture
Riemannian Geometry is the study of curved spaces. It is a powerful tool for taking local information to deduce global results, with applications across diverse areas including topology, group theory, analysis, general relativity and string theory. In these two introductory lectures
From playlist Oxford Mathematics Student Lectures - Riemannian Geometry

Riemann Roch: structure of genus 1 curves
This talk is about the Riemann Roch theorem in the spacial case of genus 1 curves or Riemann surface. We show that a compact Riemann surface satisfying the Riemann Roch theorem for g=1 is isomorphic to a nonsingular plane cubic. We show that this is topologically a torus, and use this to s
From playlist Algebraic geometry: extra topics

Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming

Gérard Besson: Some open 3-manifolds
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Some identities involving the Riemann-Zeta function.
After introducing the Riemann-Zeta function we derive a generating function for its values at positive even integers. This generating function is used to prove two sum identities. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

I give a proof of the Cartan-Hadamard theorem on non-positively curved complete Riemannian manifolds. For more details see Chapter 7 of do Carmo's "Riemannian geomety". If you find any typos or mistakes, please point them out in the comments.
From playlist Differential geometry

Lauri Oksanen: On the boundary control method
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Partial Differential Equations

Jialong Deng - Enlargeable Length-structures and Scalar Curvatures
38th Annual Geometric Topology Workshop (Online), June 15-17, 2021 Jialong Deng, University of Goettingen Title: Enlargeable Length-structures and Scalar Curvatures Abstract: We define enlargeable length-structures on closed topological manifolds and then show that the connected sum of a
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021

Geometry of Surfaces - Topological Surfaces Lecture 1 : Oxford Mathematics 3rd Year Student Lecture
This is the first of four lectures from Dominic Joyce's 3rd Year Geometry of Surfaces course. The four lectures cover topological surfaces and conclude with a big result, namely the classification of surfaces. This lecture provides an introduction to the course and to topological surfaces.
From playlist Oxford Mathematics Student Lectures - Geometry of Surfaces

Z. Badreddine - Optimal transportation problem and MCP property on sub-Riemannian structures
This presentation is devoted to the study of mass transportation on sub-Riemannian geometry. In order to obtain existence and uniqueness of optimal transport maps, the first relevant method to consider is the one used by Figalli and Rifford which is based on the local semiconcavity of the
From playlist Journées Sous-Riemanniennes 2018

Emanuel Milman: Functional Inequalities on sub-Riemannian manifolds via QCD
We are interested in obtaining Poincar ́e and log-Sobolev inequalities on domains in sub-Riemannian manifolds (equipped with their natural sub-Riemannian metric and volume measure). It is well-known that strictly sub-Riemannian manifolds do not satisfy any type of Curvature-Dimension condi
From playlist Workshop: High dimensional measures: geometric and probabilistic aspects

We present a proof of the Hopf-Rinow theorem. For more details see do Carmo's "Riemannian geometry" Chapter 7.
From playlist Differential geometry

Riemann Roch for genus 0 curves
This lecture is about the Riemann_Roch theorem in the case of genus 0 curves. This is an easy warming up exercise for the harder cases of nonzero genus as we can work everything out explicitly. We verify the Riemann-Roch theorem for the projective line (or Riemann sphere), and then use the
From playlist Algebraic geometry: extra topics
