
Proof of the existence of the minimal polynomial. Every polynomial that annihilates an operator is a polynomial multiple of the minimal polynomial of the operator. The eigenvalues of an operator are precisely the zeros of the minimal polynomial of the operator.
From playlist Linear Algebra Done Right

Matrix Representations of Fields - Lecture 04 - Field Theory
For a finite extension K of F of degree d there exists a ring map from K to d x d matrices with entries in F which is injective. This allows us to define the norm, trace, and characteristic polynomial of an element. The minimal polynomial of this associated matrix is the minimal polynomial
From playlist Field Theory

Basic/Primitive Extensions and Minimal Polynomials - Field Theory - Lecture 02
A "basic" or "primitive" extension of a field F is a new field F(alpha) where alpha in K an extension of F. We give some basic properties of extensions. Most importantly introduce the concept of minimal polynomials. @MatthewSalomone has some good videos on this already which might be mor
From playlist Field Theory

This video is about polynomials with coefficients in a field.
From playlist Basics: Field Theory

Field Theory: We consider the property of algebraic in terms of finite degree, and we define algebraic numbers as those complex numbers that are algebraic over the rationals. Then we give an overview of algebraic numbers with examples.
From playlist Abstract Algebra

Field Theory - Algebraically Closed Fields - Lecture 9
In this video we define what an algebraically closed field and assert without proof that they exist. We also explain why if you can find a single root for any polynomial, then you can find them all.
From playlist Field Theory

Visual Group Theory, Lecture 6.3: Polynomials and irreducibility
Visual Group Theory, Lecture 6.3: Polynomials and irreducibility A complex number is algebraic over Q (the rationals) if it is the root of a polynomial with rational coefficients. It is clear that every number that can be written with arithmetic and radicals is rational. Galois' big achie
From playlist Visual Group Theory

Field Theory: Irreducible Polynomials
This video is about irreducible polynomials.
From playlist Basics: Field Theory

Field Theory: We consider the case of simple extensions, where we adjoin a single element to a given field. The cases of transcendental and algebraic arise, depending on whether the kernel of the evaluation map is zero or not. In the algebraic case, we define the minimal polynomial, show
From playlist Abstract Algebra

James Freitag, University of Illinois at Chicago
March 29, James Freitag, University of Illinois at Chicago Not Pfaffian
From playlist Spring 2022 Online Kolchin seminar in Differential Algebra
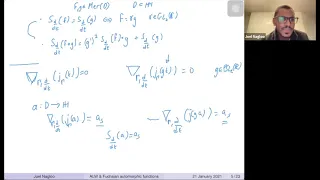
Ax-Lindemann-Weierstrass Theorem (ALW) for Fuchsian automorphic functions - Joel Nagloo
Joint IAS/Princeton University Number Theory Seminar Topic: Ax-Lindemann-Weierstrass Theorem (ALW) for Fuchsian automorphic functions Speaker: Joel Nagloo Affiliation: City University of New York Date: January 21, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Ivelisse Rubio: "Exploring, generalizing and applying the covering method"
Latinx in the Mathematical Sciences Conference 2018 "Exploring, generalizing and applying the covering method" Ivelisse Rubio, University of Puerto Rico, Rio Piedras ABSTRACT: The divisibility of exponential sums has been used to characterize and prove properties in coding theory, crypto
From playlist Latinx in the Mathematical Sciences 2018

Matthew DeVilbiss, University of Illinois at Chicago
October 28, Matthew DeVilbiss, University of Illinois at Chicago Generic Differential Equations are Strongly Minimal
From playlist Fall 2021 Online Kolchin Seminar in Differential Algebra

Functional Transcendence via Model Theory - Joel Ronnie Nagloo
CAARMS Topic: Functional Transcendence via Model Theory Speaker: Joel Ronnie Nagloo Affiliation: Bronx Community College - CUNY Date: July 12, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Elliot Kaplan, McMaster Unviersity
October 7, Elliot Kaplan, McMaster Unviersity Generic derivations on o-minimal structures
From playlist Fall 2021 Online Kolchin Seminar in Differential Algebra
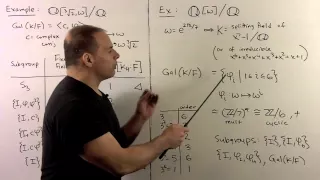
FIT4.3. Galois Correspondence 1 - Examples
Field Theory: We define Galois extensions and state the Fundamental Theorem of Galois Theory. Proofs are given in the next part; we give examples to illustrate the main ideas.
From playlist Abstract Algebra

FIT3.1.1. Roots of Polynomials
Field Theory: We recall basic factoring results for polynomials from Ring Theory and give a definition of a splitting field. This allows one to consider any irreducible polynomial as a set of roots, and in turn we consider when an irreducible polynomial can have multiple roots. We finish
From playlist Abstract Algebra
Field Theory: Fields of Order a Power of a Prime
This video is about finite fields and some of their properties.
From playlist Basics: Field Theory

Motivations, connections and scope of the workshop - Avi Wigderson
Optimization, Complexity and Invariant Theory Topic: Motivations, connections and scope of the workshop Speaker: Avi Wigderson Affiliation: Institute for Advanced Study Date: June 4, 2018 For more videos, please visit http://video.ias.edu
From playlist Optimization, Complexity and Invariant Theory