
The Additive Group of Integers Modulo n
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The Additive Group of Integers Modulo n
From playlist Abstract Algebra
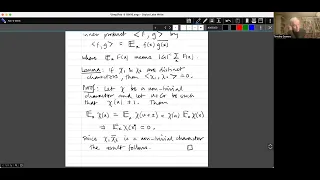
Introduction to additive combinatorics lecture 7.3 -- dual groups and the discrete Fourier transform
The discrete Fourier transform is a fundamental tool in additive combinatorics that makes it possible to prove many interesting results that would be very hard or even impossible to prove otherwise. Here I discuss the characters on a finite Abelian group G, prove that they are orthogonal a
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

The General Linear Group, The Special Linear Group, The Group C^n with Componentwise Multiplication
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The General Linear Group, The Special Linear Group, The Group C^n with Componentwise Multiplication
From playlist Abstract Algebra

AlgTopReview2: Introduction to group theory
This lecture gives a brief overview or introduction to group theory, concentrating on commutative groups (future lectures will talk about the non-commutative case). We generally use additive notation + for the operation in a commutative group, and 0 for the (additive) inverse. The main sta
From playlist Algebraic Topology

The Special Linear Group is a Subgroup of the General Linear Group Proof
The Special Linear Group is a Subgroup of the General Linear Group Proof
From playlist Abstract Algebra

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

Definition of a Cyclic Group with Examples
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Cyclic Group with Examples
From playlist Abstract Algebra

Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Subgroup in Abstract Algebra with Examples of Subgroups
From playlist Abstract Algebra

This organic chemistry video tutorial provides a basic introduction into aldehydes and ketones. Here is a list of topics: 1. Reduction of Aldehydes and Ketones With NaBH4 2. Reduction of Esters and Acid Chlorides With LiAlH4 3. Reduction of Acid Chlorides to Aldehydes Using LiAl(OR)3
From playlist New Organic Chemistry Playlist
What is a Tensor? Lesson 19: Algebraic Structures I
What is a Tensor? Lesson 19: Algebraic Structures Part One: Groupoids to Fields This is a redo or a recently posted lesson. Same content, a bit cleaner. Algebraic structures are frequently mentioned in the literature of general relativity, so it is good to understand the basic lexicon of
From playlist What is a Tensor?

Yonatan Harpaz - New perspectives in hermitian K-theory II
Warning: around 32:30 in the video, in the slide entitled "Karoubi's conjecture", a small mistake was made - in the third bulleted item the genuine quadratic structure appearing should be the genuine symmetric one (so both the green and red instances of the superscript gq should be gs), an
From playlist New perspectives on K- and L-theory

Organic Chemistry - Reaction Mechanisms - Addition, Elimination, Substitution, & Rearrangement
This organic chemistry video tutorial provides a basic introduction into reaction mechanisms. It explains the four fundamental reactions such as addition reactions, elimination reactions, substitution reactions, and rearrangements. Here is a list of topics: 1. Electrophilic Addition R
From playlist New Organic Chemistry Playlist

Elliptic Curves - Lecture 16a - Formal groups and their homomorphisms
This video is part of a graduate course on elliptic curves that I taught at UConn in Spring 2021. The course is an introduction to the theory of elliptic curves. More information about the course can be found at the course website: https://alozano.clas.uconn.edu/math5020-elliptic-curves/
From playlist An Introduction to the Arithmetic of Elliptic Curves

Yonatan Harpaz - New perspectives in hermitian K-theory III
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics Münster: https://go.wwu
From playlist New perspectives on K- and L-theory

Lec 8 | MIT 6.451 Principles of Digital Communication II
Introduction to Finite Fields View the complete course: http://ocw.mit.edu/6-451S05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.451 Principles of Digital Communication II

Abstract Algebra - 3.1 Finite Groups and Subgroups: Terminology and Notation
Most of this chapter will revolve around the idea of a subgroup. However, we must begin by being able to differentiate between a finite group and infinite group. We look at some notation and definitions (order of a group, order of an element) before jumping into subgroups. Video Chapters:
From playlist Abstract Algebra - Entire Course

What is a Group? | Abstract Algebra
Welcome to group theory! In today's lesson we'll be going over the definition of a group. We'll see the four group axioms in action with some examples, and some non-examples as well which violate the axioms and are thus not groups. In a fundamental way, groups are structures built from s
From playlist Abstract Algebra

Definition of a Ring and Examples of Rings
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Ring and Examples of Rings - Definition of a Ring. - Definition of a commutative ring and a ring with identity. - Examples of Rings include: Z, Q, R, C under regular addition and multiplication The Ring of all n x
From playlist Abstract Algebra

Michael Wibmer: Etale difference algebraic groups
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry