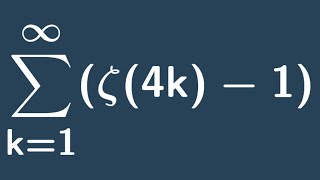
More identities involving the Riemann-Zeta function!
By applying some combinatorial tricks to an identity from https://youtu.be/2W2Ghi9idxM we are able to derive two identities involving the Riemann-Zeta function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

Some identities involving the Riemann-Zeta function.
After introducing the Riemann-Zeta function we derive a generating function for its values at positive even integers. This generating function is used to prove two sum identities. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

Mark Pollicott - Dynamical Zeta functions (Part 2)
Dynamical Zeta functions (Part 1) Licence: CC BY NC-ND 4.0
From playlist École d’été 2013 - Théorie des nombres et dynamique

Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming

A crash course in Algebraic Number Theory
A quick proof of the Prime Ideal Theorem (algebraic analog of the Prime Number Theorem) is presented. In algebraic number theory, the prime ideal theorem is the number field generalization of the prime number theorem. It provides an asymptotic formula for counting the number of prime idea
From playlist Number Theory
James Arthur - Zeta functions and orbital integrals
We shall review the work of Z. Yun on zeta functions of orders, and of A. Altug on elliptic terms in the trace formula for GL(2). We shall then study the problem of Poisson summation for general linear groups. A suitable solution would be an important step in Langlands' proposed reformula
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Transcendental Functions 17 The Indefinite Integral of 1 over u du Example 1.mov
Example problems involving the integral of u to the power negative 1 du.
From playlist Transcendental Functions

Andrew Sutherland, Arithmetic L-functions and their Sato-Tate distributions
VaNTAGe seminar on April 28, 2020. License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

Transcendental Functions 19 The Function a to the power x.mp4
The function a to the power x.
From playlist Transcendental Functions

Transcendental Functions 3 Examples using Properties of Logarithms.mov
Examples using the properties of logarithms.
From playlist Transcendental Functions

[ANT13] Dedekind domains, integral closure, discriminants... and some other loose ends
In this video, we see an example of how badly this theory can fail in a non-Dedekind domain, and so - regrettably - we finally break our vow of not learning what a Dedekind domain is.
From playlist [ANT] An unorthodox introduction to algebraic number theory

Monotonicity of the Riemann zeta function and related functions - P Zvengrowski [2012]
General Mathematics Seminar of the St. Petersburg Division of Steklov Institute of Mathematics, Russian Academy of Sciences May 17, 2012 14:00, St. Petersburg, POMI, room 311 (27 Fontanka) Monotonicity of the Riemann zeta function and related functions P. Zvengrowski University o
From playlist Number Theory

From playlist Atelier PARI/GP 2016

CTNT 2020 - The global field Euler function. Santiago Arango-Piñeros.
The paper is available at https://arxiv.org/abs/2005.04521?fbclid=IwAR34njBRG6gEAjzQqdk7johkPEC5i4c5Bbq1MJtyeNAZ95yeQWvaiys2LF0 Comments very welcome!
From playlist CTNT 2020 - Conference Videos

The rising sea: Grothendieck on simplicity and generality - Colin McLarty [2003]
Slides for this talk: https://drive.google.com/file/d/1yDmqhdcKo6-YpDpRdHh2hvuNirZVbcKr/view?usp=sharing Notes for this talk: https://drive.google.com/open?id=1p45B3Hh8WPRhdhQAd0Wq0MvmY0JYSnmc The History of Algebra in the Nineteenth and Twentieth Centuries April 21 - 25, 2003 Colin Mc
From playlist Mathematics
Henri Cohen - Introduction to asymptotics of number fields... [2011]
Introduction to asymptotics of number fields, conjectures, computation, experiments Introductory Workshop: Arithmetic Statistics January 31, 2011 - February 04, 2011 January 31, 2011 (09:10 AM PST - 10:10 AM PST) Speaker(s): Henri Cohen Location: MSRI: Simons Auditorium http://www.msri.
From playlist Number Theory

Transcendental Functions 17 The Indefinite Integral of 1 over u du Example 2.mov
More example problems involving the integral of 1 over u, du.
From playlist Transcendental Functions

CTNT 2018 - "The Tsfasman-Vladut Generalization of the Brauer-Siegel Theorem" by Farshid Hajir
This is lecture on "The Tsfasman-Vladut Generalization of the Brauer-Siegel Theorem", by Farshid Hajir (UMass Amherst), during CTNT 2018, the Connecticut Summer School in Number Theory. For more information about CTNT and other resources and notes, see https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2018 - Guest Lectures
