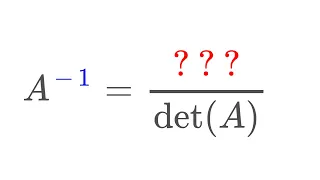
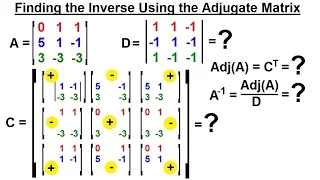
In this video, I define the notion of adjugate matrix and use it to calculate A-1 using determinants. This is again beautiful in theory, but inefficient in examples. Adjugate matrix example: https://youtu.be/OFykHi0idnQ Check out my Determinants Playlist: https://www.youtube.com/playlist
From playlist Determinants

Matrices | Adjoint of a Matrix | Don't Memorise
What is the Adjoint of a Matrix? To learn more about, Matrices, enroll in our full course now: https://infinitylearn.com/microcourses?utm_source=youtube&utm_medium=Soical&utm_campaign=DM&utm_content=2ugSvI-F__I&utm_term=%7Bkeyword%7D In this video, we will learn: 0:00 how to find adjoin
From playlist Matrices

Matrices | Adjoint of a Matrix (Examples) | Don't Memorise
What is the Adjoint of a Matrix? ✅To learn more about, Matrices, enroll in our full course now: https://infinitylearn.com/microcourses?utm_source=youtube&utm_medium=Soical&utm_campaign=DM&utm_content=hiuqyvR-f_4&utm_term=%7Bkeyword%7D In this video, we will learn: 0:00 how to find adjo
From playlist Matrices

Linear Algebra: Ch 2 - Determinants (46 of 48) Find Inverse Using the Adjugate Matrix (2x2)
Visit http://ilectureonline.com for more math and science lectures! In this video I will find the inverse of a 2x2 matrix using the adjugate matrix. Next video in this series can be seen at: https://youtu.be/5rNgonlmPKs
From playlist LINEAR ALGEBRA 2: DETERMINANTS
Linear Algebra: Ch 2 - Determinants (45 of 48) Find Inverse Using the Adjugate Matrix (3x3)
Visit http://ilectureonline.com for more math and science lectures! In this video I will find the inverse of a 3x3 matrix using the adjugate matrix. Next video in this series can be seen at: https://youtu.be/qasuxxoMt0A
From playlist LINEAR ALGEBRA 2: DETERMINANTS

Algebra 1M - international Course no. 104016 Dr. Aviv Censor Technion - International school of engineering
From playlist Algebra 1M

Classic video on inverting a 3x3 matrix part 1 | Matrices | Precalculus | Khan Academy
Inverting a 3x3 matrix Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/e/matrix_inverse_3x3?utm_source=YTdescription&utm_medium=YTdescription&utm_campaign=YTdescription Watch the next lesson: https://www.khanacademy.org/math/precalculus/precalc-ma
From playlist Matrices | Precalculus | Khan Academy

Inverting 3x3 part 2: Determinant and adjugate of a matrix | Matrices | Precalculus | Khan Academy
Finishing up our 3x3 matrix inversion Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/precalculus/precalc-matrices/inverting_matrices/e/matrix_inverse_3x3?utm_source=YT&utm_medium=Desc&utm_campaign=Precalculus Watch the next lesson: https://w
From playlist Matrices | Precalculus | Khan Academy

Inverse of 3 x 3 Matrix Using Adjugate Formula
Linear Algebra: Find the inverse of the 3 x 3 matrix A = [ \ \ ] using the adjugate (or classical adjoint) of A. This is mostly a bookkeeping exercise.
From playlist MathDoctorBob: Linear Algebra I: From Linear Equations to Eigenspaces | CosmoLearning.org Mathematics

How do we add matrices. A matrix is an abstract object that exists in its own right, and in this sense, it is similar to a natural number, or a complex number, or even a polynomial. Each element in a matrix has an address by way of the row in which it is and the column in which it is. Y
From playlist Introducing linear algebra
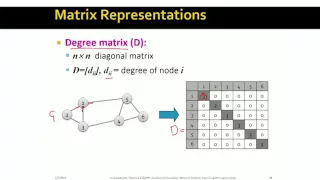
Graph Representation with an Adjacency Matrix | Graph Theory, Adjaceny Matrices
How do we represent graphs using adjacency matrices? That is the subject of today's graph theory lesson! We will take a graph and use an adjacency matrix to represent it! It is a most soulless, but at times useful, graph representation. An adjacency matrix has a row and a column for each
From playlist Graph Theory

Inverse of 4x4 Matrix Using Adjugate Formula
Typo around 4:15. In the cofactor grid, the matrix in the first column, third row, C(3,1) should have bottom row (0, 1, 4), not (2, 1, 4). This is a typo, as the following work uses the correct numbers. (Thanks to Amin Haddad!) Linear Algebra: We find the inverse of a 4x4 matrix usin
From playlist MathDoctorBob: Linear Algebra I: From Linear Equations to Eigenspaces | CosmoLearning.org Mathematics

Inverse Matrices and Their Properties
We learned about matrix multiplication, so what about matrix division? There is no such thing! But we can multiply a matrix by its inverse, which is kind of like multiplying a number by its reciprocal, to cancel it out, which with matrices will yield the identity matrix. So how do you find
From playlist Mathematics (All Of It)

What is a matrix? Free ebook http://tinyurl.com/EngMathYT
From playlist Intro to Matrices

Matrix Addition, Subtraction, and Scalar Multiplication
This video shows how to add, subtract and perform scalar multiplication with matrices. http://mathispower4u.yolasite.com/ http://mathispower4u.wordpress.com/
From playlist Introduction to Matrices and Matrix Operations

Inverse of a 2x2 matrix | Matrices | Precalculus | Khan Academy
Courses on Khan Academy are always 100% free. Start practicing—and saving your progress—now: https://www.khanacademy.org/math/precalculus/x9e81a4f98389efdf:matrices/x9e81a4f98389efdf:practice-finding-inverses-of-2x2-matrices/v/inverse-of-a-2x2-matrix Example of calculating the inverse of
From playlist Matrices | Precalculus | Khan Academy