
On the Setoid Model of Type Theory - Erik Palmgren
Erik Palmgren University of Stockholm October 18, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Natural Models of Type Theory - Steve Awodey
Steve Awodey Carnegie Mellon University; Member, School of Mathematics March 28, 2013 For more videos, visit http://video.ias.edu
From playlist Mathematics

LambdaConf 2015 - Type Theory and its Meaning Explanations Jon Sterling
At the heart of intuitionistic type theory lies an intuitive semantics called the “meaning explanations." Crucially, when meaning explanations are taken as definitive for type theory, the core notion is no longer “proof” but “verification”. We’ll explore how type theories of this sort aris
From playlist LambdaConf 2015

David McAllester - Dependent Type Theory from the Perspective of Mathematics, Physics, and (...)
Dependent type theory imposes a type system on Zemelo-Fraenkel set theory (ZFC). From a mathematics and physics perspective dependent type theory naturally generalizes the Bourbaki notion of structure and provides a universal notion of isomorphism and symmetry. This comes with a universal
From playlist Mikefest: A conference in honor of Michael Douglas' 60th birthday

There are two different types of reductionism. One is called methodological reductionism, the other one theory reductionism. Methodological reductionism is about the properties of the real world. It’s about taking things apart into smaller things and finding that the smaller things determ
From playlist Philosophy of Science

Andrej Bauer and Peter LeFanu Lumsdaine: Toward an initiality theorem for general type theories
The lecture was held within the framework of the Hausdorff Trimester Program: Types, Sets and Constructions. Abstract: I will report on a project of defining carefully and formally what a general type theory is. This is kind of step 1 to a generally applicable initiality theorem. It's not
From playlist Workshop: "Types, Homotopy, Type theory, and Verification"

Constructive Type Theory and Homotopy - Steve Awodey
Steve Awodey Institute for Advanced Study December 3, 2010 In recent research it has become clear that there are fascinating connections between constructive mathematics, especially as formulated in the type theory of Martin-Löf, and homotopy theory, especially in the modern treatment in
From playlist Mathematics
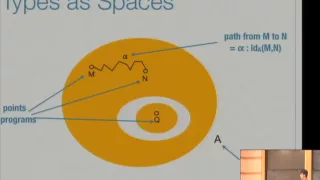
Computing with Univalence - Daniel Licata
Daniel Licata Carnegie Mellon University; Member, School of Mathematics September 28, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Univalent Foundations Seminar - Steve Awodey
Steve Awodey Carnegie Mellon University; Member, School of Mathematics November 19, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

On Voevodsky's univalence principle - André Joyal
Vladimir Voevodsky Memorial Conference Topic: On Voevodsky's univalence principle Speaker: André Joyal Affiliation: Université du Québec á Montréal Date: September 11, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics

Why Algebraic Data Types Are Important
Strong static typing detects a lot of bugs at compile time, so why would anyone prefer to program in JavaScript or Python? The main reason is that type systems can be extremely complex, often with byzantine typing rules (C++ comes to mind). This makes generic programming a truly dark art.
From playlist Functional Programming

Programming with Math (Exploring Type Theory)
As programs are getting more complex, it's time to go back to basics, to the old well tested approach to complexity called mathematics. Let compilers deal with the intricacies of Turing machines. Our strength is abstract thinking. Let's use it! EVENT: Øredev 2018 SPEAKER: Bartosz Milew
From playlist Software Development

Homotopy Group - (1)Dan Licata, (2)Guillaume Brunerie, (3)Peter Lumsdaine
(1)Carnegie Mellon Univ.; Member, School of Math, (2)School of Math., IAS, (3)Dalhousie Univ.; Member, School of Math April 11, 2013 In this general survey talk, we will describe an approach to doing homotopy theory within Univalent Foundations. Whereas classical homotopy theory may be des
From playlist Mathematics

The synthetic theory of ∞-categories vs the synthetic theory of ∞-categories - Emily Riehl
Vladimir Voevodsky Memorial Conference Topic: The synthetic theory of ∞-categories vs the synthetic theory of ∞-categories Speaker: Emily Riehl Affiliation: Johns Hopkins University Date: September 12, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics

Séminaire Bourbaki - 21/06/2014 - 4/4 - Thierry COQUAND
Théorie des types dépendants et axiome d'univalence Cet exposé sera une introduction à la théorie des types dépendants et à l'axiome d'univalence. Cette théorie est une alternative à la théorie des ensembles comme fondement des mathématiques. Guidé par une interprétation d'un type comme u
From playlist Bourbaki - 21 juin 2014

Type Systems - Vladimir Voevodsky
Vladimir Voevodsky Institute for Advanced Study November 21, 2012
From playlist Mathematics


