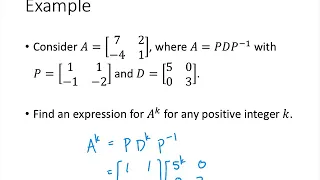Diagonalizable matrix
In linear algebra, a square matrix is called diagonalizable or non-defective if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix and a diagonal matrix such that , or equivalently . (Such , are not unique.) For a finite-dimensional vector space , a linear map is called diagonalizable if there exists an ordered basis of consisting of eigenvectors of . These definitions are equivalent: if has a matrix representation as above, then the column vectors of form a basis consisting of eigenvectors of , and the diagonal entries of are the corresponding eigenvalues of ; with respect to this eigenvector basis, is represented by . Diagonalization is the process of finding the above and . Diagonalizable matrices and maps are especially easy for computations, once their eigenvalues and eigenvectors are known. One can raise a diagonal matrix to a power by simply raising the diagonal entries to that power, and the determinant of a diagonal matrix is simply the product of all diagonal entries; such computations generalize easily to . Geometrically, a diagonalizable matrix is an inhomogeneous dilation (or anisotropic scaling) — it scales the space, as does a homogeneous dilation, but by a different factor along each eigenvector axis, the factor given by the corresponding eigenvalue. A square matrix that is not diagonalizable is called defective. It can happen that a matrix with real entries is defective over the real numbers, meaning that is impossible for any invertible and diagonal with real entries, but it is possible with complex entries, so that is diagonalizable over the complex numbers. For example, this is the case for a generic rotation matrix. Many results for diagonalizable matrices hold only over an algebraically closed field (such as the complex numbers). In this case, diagonalizable matrices are dense in the space of all matrices, which means any defective matrix can be deformed into a diagonalizable matrix by a small perturbation; and the Jordan normal form theorem states that any matrix is uniquely the sum of a diagonalizable matrix and a nilpotent matrix. Over an algebraically closed field, diagonalizable matrices are equivalent to semi-simple matrices. (Wikipedia).