6-polytope
In six-dimensional geometry, a six-dimensional polytope or 6-polytope is a polytope, bounded by 5-polytope facets. (Wikipedia).
In six-dimensional geometry, a six-dimensional polytope or 6-polytope is a polytope, bounded by 5-polytope facets. (Wikipedia).
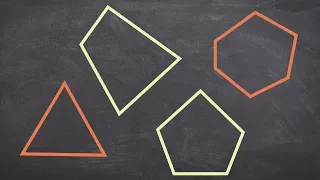
What are four types of polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Illustrative Mathematics Grade 6 - Unit 1- Lesson 13
Illustrative Mathematics Grade 6 - Unit 1- Lesson 13 Open Up Resources (OUR) If you have any questions, please contact me at dhabecker@gmail.com
From playlist Illustrative Mathematics Grade 6 Unit 1

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What are the names of different types of polygons based on the number of sides
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Classifying a polygon in two different ways ex 4
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Tropical Geometry - Lecture 8 - Surfaces | Bernd Sturmfels
Twelve lectures on Tropical Geometry by Bernd Sturmfels (Max Planck Institute for Mathematics in the Sciences | Leipzig, Germany) We recommend supplementing these lectures by reading the book "Introduction to Tropical Geometry" (Maclagan, Sturmfels - 2015 - American Mathematical Society)
From playlist Twelve Lectures on Tropical Geometry by Bernd Sturmfels

Tropical Geometry - Lecture 12 - Geometric Tropicalization | Bernd Sturmfels
Twelve lectures on Tropical Geometry by Bernd Sturmfels (Max Planck Institute for Mathematics in the Sciences | Leipzig, Germany) We recommend supplementing these lectures by reading the book "Introduction to Tropical Geometry" (Maclagan, Sturmfels - 2015 - American Mathematical Society)
From playlist Twelve Lectures on Tropical Geometry by Bernd Sturmfels

Perfect Shapes in Higher Dimensions - Numberphile
Carlo Sequin talks through platonic solids and regular polytopes in higher dimensions. More links & stuff in full description below ↓↓↓ Extra footage (Hypernom): https://youtu.be/unC0Y3kv0Yk More videos with with Carlo: http://bit.ly/carlo_videos Edit and animation by Pete McPartlan Pete
From playlist Carlo Séquin on Numberphile

Tropical Geometry - Lecture 7 - Linear Spaces | Bernd Sturmfels
Twelve lectures on Tropical Geometry by Bernd Sturmfels (Max Planck Institute for Mathematics in the Sciences | Leipzig, Germany) We recommend supplementing these lectures by reading the book "Introduction to Tropical Geometry" (Maclagan, Sturmfels - 2015 - American Mathematical Society)
From playlist Twelve Lectures on Tropical Geometry by Bernd Sturmfels

AlgTop9: Applications of Euler's formula and graphs
We use Euler's formula to show that there are at most 5 Platonic, or regular, solids. We discuss other types of polyhedra, including deltahedra (made of equilateral triangles) and Schafli's generalizations to higher dimensions. In particular in 4 dimensions there is the 120-cell, the 600-c
From playlist Algebraic Topology: a beginner's course - N J Wildberger
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Nonlinear algebra, Lecture 13: "Polytopes and Matroids ", by Mateusz Michalek
This is the thirteenth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Panorama of Mathematics: Michel Goemans
Panorama of Mathematics To celebrate the tenth year of successful progression of our cluster of excellence we organized the conference "Panorama of Mathematics" from October 21-23, 2015. It outlined new trends, results, and challenges in mathematical sciences. Michel Goemans: "A Panorami
From playlist Panorama of Mathematics

Karim Alexander Adiprasito: New Construction for projectively unique polytopes
K. Adiprasitos lecture was held within the framework of the Hausdorff Trimester Program Universality and Homogeneity during the special seminar "Universality of moduli spaces and geometry" (06.11.2013)
From playlist HIM Lectures: Trimester Program "Universality and Homogeneity"

Anja Fischer: Polynomial Matroid Optimisation Problems
n this talk we consider polynomial matroid optimisation problems with some non-linear monomials in the objective function. The monomials are linearised and we study the corresponding polytopes. Extending results of Edmonds we present complete descriptions for the linearised polytopes for t
From playlist HIM Lectures: Trimester Program "Combinatorial Optimization"

What is a polygon and what is a non example of a one
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Tropical Geometry - Lecture 11 - Toric Varieties | Bernd Sturmfels
Twelve lectures on Tropical Geometry by Bernd Sturmfels (Max Planck Institute for Mathematics in the Sciences | Leipzig, Germany) We recommend supplementing these lectures by reading the book "Introduction to Tropical Geometry" (Maclagan, Sturmfels - 2015 - American Mathematical Society)
From playlist Twelve Lectures on Tropical Geometry by Bernd Sturmfels