
What is the definition of a ray
👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

Shapes, faces, edges, vertices - G3
Break down of the parts of three dimensional shapes, including: cubes, right triangular prisms, rectangular prisms, cylinders, cones and square pyramids.
From playlist Geometry: 3D

What is a Ray and how do we label one
👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

Light and Optics 5_1 Refractive Surfaces
The bending of light rays at the interface of refracting surfaces.
From playlist Physics - Light and Optics

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

ggplot2 Tutorial | ggplot2 In R Tutorial | Data Visualization In R | R Training | Edureka
( R Training : https://www.edureka.co/data-analytics-with-r-certification-training ) This "ggplot2 Tutorial" by Edureka is a comprehensive session on the ggplot2 in R. This tutorial will not only get you started with the ggplot2 package, but also make you an expert in visualizing data wit
From playlist Data Science Tutorial Videos
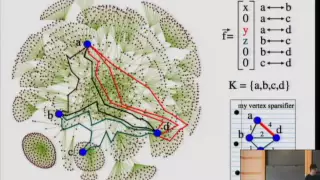
The (Counter-Intuitive) Geometry of Cut and Flow Polytopes - Ankur Moitra
Ankur Moitra Massachusetts Institute of Technology; Institute for Advanced Study October 3, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

Stephan Weltge: Binary scalar products
We settle a conjecture by Bohn, Faenza, Fiorini, Fisikopoulos, Macchia, and Pashkovich (2015) concerning 2-level polytopes. Such polytopes have the property that for every facet-defining hyperplane H there is a parallel hyperplane H0 such that H and H0 contain all vertices. The authors con
From playlist Workshop: Tropical geometry and the geometry of linear programming

Representations of Fuchsian groups, parahoric group schemes by Vikraman Balaji
DISCUSSION MEETING : MODULI OF BUNDLES AND RELATED STRUCTURES ORGANIZERS : Rukmini Dey and Pranav Pandit DATE : 10 February 2020 to 14 February 2020 VENUE : Ramanujan Lecture Hall, ICTS, Bangalore Background: At its core, much of mathematics is concerned with the problem of classif
From playlist Moduli Of Bundles And Related Structures 2020

OpenGL - PBR (physically based rendering)
Code samples derived from work by Joey de Vries, @joeydevries, author of https://learnopengl.com/ All code samples, unless explicitly stated otherwise, are licensed under the terms of the CC BY-NC 4.0 license as published by Creative Commons, either version 4 of the License, or (at your o
From playlist OpenGL

Lagrangian Floer theory (Lecture – 02) by Sushmita Venugopalan
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

Symplectic Vortices and the Quantum Kirwan Map (Lecture 1) by Chris Woodward
PROGRAM: VORTEX MODULI ORGANIZERS: Nuno Romão (University of Augsburg, Germany) and Sushmita Venugopalan (IMSc, India) DATE & TIME: 06 February 2023 to 17 February 2023 VENUE: Ramanujan Lecture Hall, ICTS Bengaluru For a long time, the vortex equations and their associated self-dual fie
From playlist Vortex Moduli - 2023

BAG1.6. Toric Varieties 6 - Faces and Localization
Basic Algebraic Geometry: We give an overview of convex geometry for polyhedral cones, including Gordan's Lemma and the Separation Lemma. A first connection to toric varieties is given by localization.
From playlist Basic Algebraic Geometry

Daniel Dadush: Probabilistic analysis of the simpler method and polytope diameter
In this talk, I will overview progress in our probabilistic understanding of the (shadow vertex) simplex method in three different settings: smoothed polytopes (whose data is randomly perturbed), well-conditioned polytopes (e.g., TU systems), and random polytopes with constraints drawn uni
From playlist Workshop: Tropical geometry and the geometry of linear programming

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

Spectrahedral lifts of convex sets – Rekha Thomas – ICM2018
Control Theory and Optimization Invited Lecture 16.6 Spectrahedral lifts of convex sets Rekha Thomas Abstract: Efficient representations of convex sets are of crucial importance for many algorithms that work with them. It is well-known that sometimes, a complicated convex set can be expr
From playlist Control Theory and Optimization
