5-polytope
In geometry, a five-dimensional polytope (or 5-polytope) is a polytope in five-dimensional space, bounded by (4-polytope) facets, pairs of which share a polyhedral cell. (Wikipedia).
In geometry, a five-dimensional polytope (or 5-polytope) is a polytope in five-dimensional space, bounded by (4-polytope) facets, pairs of which share a polyhedral cell. (Wikipedia).

What are four types of polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons
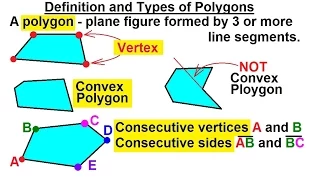
Geometry - Basic Terminology (11 of 34) Definition of Polygons and Convex Polygons
Visit http://ilectureonline.com for more math and science lectures! In this video I will define what are polygons and convex polygons. Next video in the Basic Terminology series can be seen at: http://youtu.be/N3wvmbsaFwQ
From playlist GEOMETRY 1 - BASIC TERMINOLOGY

Illustrative Mathematics Grade 6 - Unit 1- Lesson 13
Illustrative Mathematics Grade 6 - Unit 1- Lesson 13 Open Up Resources (OUR) If you have any questions, please contact me at dhabecker@gmail.com
From playlist Illustrative Mathematics Grade 6 Unit 1

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the difference between convex and concave
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Classifying a polygon in two different ways ex 4
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What are the names of different types of polygons based on the number of sides
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Tropical Geometry - Lecture 9 - Tropical Convexity | Bernd Sturmfels
Twelve lectures on Tropical Geometry by Bernd Sturmfels (Max Planck Institute for Mathematics in the Sciences | Leipzig, Germany) We recommend supplementing these lectures by reading the book "Introduction to Tropical Geometry" (Maclagan, Sturmfels - 2015 - American Mathematical Society)
From playlist Twelve Lectures on Tropical Geometry by Bernd Sturmfels

Perfect Shapes in Higher Dimensions - Numberphile
Carlo Sequin talks through platonic solids and regular polytopes in higher dimensions. More links & stuff in full description below ↓↓↓ Extra footage (Hypernom): https://youtu.be/unC0Y3kv0Yk More videos with with Carlo: http://bit.ly/carlo_videos Edit and animation by Pete McPartlan Pete
From playlist Carlo Séquin on Numberphile

Tropical Geometry - Lecture 12 - Geometric Tropicalization | Bernd Sturmfels
Twelve lectures on Tropical Geometry by Bernd Sturmfels (Max Planck Institute for Mathematics in the Sciences | Leipzig, Germany) We recommend supplementing these lectures by reading the book "Introduction to Tropical Geometry" (Maclagan, Sturmfels - 2015 - American Mathematical Society)
From playlist Twelve Lectures on Tropical Geometry by Bernd Sturmfels

Zakhar Kabluchko: Random Polytopes, Lecture III
In these three lectures we will provide an introduction to the subject of beta polytopes. These are random polytopes defined as convex hulls of i.i.d. samples from the beta density proportional to (1 − ∥x∥2)β on the d-dimensional unit ball. Similarly, beta’ polytopes are defined as convex
From playlist Workshop: High dimensional spatial random systems

Tropical Geometry - Lecture 8 - Surfaces | Bernd Sturmfels
Twelve lectures on Tropical Geometry by Bernd Sturmfels (Max Planck Institute for Mathematics in the Sciences | Leipzig, Germany) We recommend supplementing these lectures by reading the book "Introduction to Tropical Geometry" (Maclagan, Sturmfels - 2015 - American Mathematical Society)
From playlist Twelve Lectures on Tropical Geometry by Bernd Sturmfels

Karim Alexander Adiprasito: New Construction for projectively unique polytopes
K. Adiprasitos lecture was held within the framework of the Hausdorff Trimester Program Universality and Homogeneity during the special seminar "Universality of moduli spaces and geometry" (06.11.2013)
From playlist HIM Lectures: Trimester Program "Universality and Homogeneity"

Circular Fence Posets and Associated Polytopes with Unexpected Symmetry by Mohan Ravichandran
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS: Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE & TIME: 27 June 2022 to 08 July 2022 VENUE: Madhava Lecture Hall and Online Algebraic geometry is t
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)

From Gentle algebras to S-matrix in Quantum Field Theory by Alok Laddha
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE: 27 June 2022 to 08 July 2022 VENUE: Madhava Lecture Hall and Online Algebraic geometry is the study of
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)

AlgTop9: Applications of Euler's formula and graphs
We use Euler's formula to show that there are at most 5 Platonic, or regular, solids. We discuss other types of polyhedra, including deltahedra (made of equilateral triangles) and Schafli's generalizations to higher dimensions. In particular in 4 dimensions there is the 120-cell, the 600-c
From playlist Algebraic Topology: a beginner's course - N J Wildberger

Panorama of Mathematics: Michel Goemans
Panorama of Mathematics To celebrate the tenth year of successful progression of our cluster of excellence we organized the conference "Panorama of Mathematics" from October 21-23, 2015. It outlined new trends, results, and challenges in mathematical sciences. Michel Goemans: "A Panorami
From playlist Panorama of Mathematics
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons