Euclidean solid geometry | Rotational symmetry | Lie groups | Rotation in three dimensions
3D rotation group
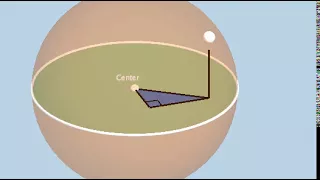
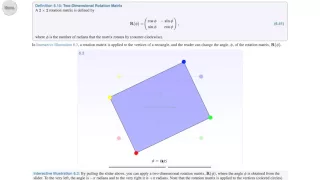
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition. By definition, a rotation about the origin is a transformation that preserves the origin, Euclidean distance (so it is an isometry), and orientation (i.e., handedness of space). Composing two rotations results in another rotation, every rotation has a unique inverse rotation, and the identity map satisfies the definition of a rotation. Owing to the above properties (along composite rotations' associative property), the set of all rotations is a group under composition. Every non-trivial rotation is determined by its axis of rotation (a line through the origin) and its angle of rotation. Rotations are not commutative (for example, rotating R 90° in the x-y plane followed by S 90° in the y-z plane is not the same as S followed by R), making the 3D rotation group a nonabelian group. Moreover, the rotation group has a natural structure as a manifold for which the group operations are smoothly differentiable, so it is in fact a Lie group. It is compact and has dimension 3. Rotations are linear transformations of and can therefore be represented by matrices once a basis of has been chosen. Specifically, if we choose an orthonormal basis of , every rotation is described by an orthogonal 3 × 3 matrix (i.e., a 3 × 3 matrix with real entries which, when multiplied by its transpose, results in the identity matrix) with determinant 1. The group SO(3) can therefore be identified with the group of these matrices under matrix multiplication. These matrices are known as "special orthogonal matrices", explaining the notation SO(3). The group SO(3) is used to describe the possible rotational symmetries of an object, as well as the possible orientations of an object in space. Its representations are important in physics, where they give rise to the elementary particles of integer spin. (Wikipedia).