
We show the connection between the method of adjoints in optimal control to the implicit function theorem ansatz. We relate the costate or adjoint state variable to Lagrange multipliers.
From playlist There and Back Again: A Tale of Slopes and Expectations (NeurIPS-2020 Tutorial)
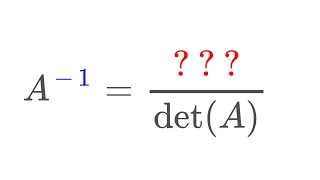
In this video, I define the notion of adjugate matrix and use it to calculate A-1 using determinants. This is again beautiful in theory, but inefficient in examples. Adjugate matrix example: https://youtu.be/OFykHi0idnQ Check out my Determinants Playlist: https://www.youtube.com/playlist
From playlist Determinants
Graph Representation with an Adjacency Matrix | Graph Theory, Adjaceny Matrices
How do we represent graphs using adjacency matrices? That is the subject of today's graph theory lesson! We will take a graph and use an adjacency matrix to represent it! It is a most soulless, but at times useful, graph representation. An adjacency matrix has a row and a column for each
From playlist Graph Theory

Matrices | Adjoint of a Matrix (Examples) | Don't Memorise
What is the Adjoint of a Matrix? ✅To learn more about, Matrices, enroll in our full course now: https://infinitylearn.com/microcourses?utm_source=youtube&utm_medium=Soical&utm_campaign=DM&utm_content=hiuqyvR-f_4&utm_term=%7Bkeyword%7D In this video, we will learn: 0:00 how to find adjo
From playlist Matrices

Algebraic properties of the adjoint. Null space and range of the adjoint. The matrix of T* is the conjugate transpose of the matrix of T.
From playlist Linear Algebra Done Right

Matrices | Adjoint of a Matrix | Don't Memorise
What is the Adjoint of a Matrix? To learn more about, Matrices, enroll in our full course now: https://infinitylearn.com/microcourses?utm_source=youtube&utm_medium=Soical&utm_campaign=DM&utm_content=2ugSvI-F__I&utm_term=%7Bkeyword%7D In this video, we will learn: 0:00 how to find adjoin
From playlist Matrices

Adjoint / Daggered Operators in Quantum Mechanics
In this video, we will explain adjoint operators in quantum mechanics. First of all, for any operator A, we can define its adjoint, A-dagger, via this equation. The idea behind this is, that while operators in quantum mechanics usually act towards the right, adjoint operators act to the le
From playlist Quantum Mechanics, Quantum Field Theory

Lara Ismert: "Heisenberg Pairs on Hilbert C*-modules"
Actions of Tensor Categories on C*-algebras 2021 "Heisenberg Pairs on Hilbert C*-modules" Lara Ismert - Embry-Riddle Aeronautical University, Mathematics Abstract: Roughly speaking, a Heisenberg pair on a Hilbert space is a pair of self-adjoint operators (A,B) which satisfy the Heisenber
From playlist Actions of Tensor Categories on C*-algebras 2021

Parahoric Subgroups and Supercuspidal Representations of p-Adic groups - Dick Gross
Dick Gross Harvard University December 9, 2010 This is a report on some joint work with Mark Reeder and Jiu-Kang Yu. I will review the theory of parahoric subgroups and consider the induced representation of a one-dimensional character of the pro-unipotent radical. A surprising fact is th
From playlist Mathematics

Lecture 18: The Adjoint of a Bounded Linear Operator on a Hilbert Space
MIT 18.102 Introduction to Functional Analysis, Spring 2021 Instructor: Dr. Casey Rodriguez View the complete course: https://ocw.mit.edu/courses/18-102-introduction-to-functional-analysis-spring-2021/ YouTube Playlist: https://www.youtube.com/watch?v=BctaYoR9tOY&list=PLUl4u3cNGP63micsJp_
From playlist MIT 18.102 Introduction to Functional Analysis, Spring 2021
Lazaro Recht: Metric geometry in homogeneous spaces of the unitary group of a C* -algebra. 2
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Lucas Mason-Brown - Arthur's Conjectures and the Orbit Method for Real Reductive Groups
The most fundamental unsolved problem in the representation theory of Lie groups is the Problem of the Unitary Dual: given a reductive Lie group G, this problem asks for a parameterization of the set of irreducible unitary G-representations. There are two big "philosophies" for approaching
From playlist 2022 Summer School on the Langlands program

The Inverse of a 2 by 2 Matrix Using the Adjoint Method
This video explains how to find the inverse matrix of a 2 by 2 matrix using the adjoint method.
From playlist Inverse Matrices

In this video I talk about a beautiful family of adjoint functors between module categories, and how these offer a natural inspiration for the definitions of induced representation, and Frobenius reciprocity.
From playlist Miscellaneous Questions

Section 3b Adjacency Matrix and Incidence Matrix
This video is about Section 3b Adjacency Matrix and Incidence Matrix
From playlist Graph Theory

Sept. 17, Chapter 4 (Linear algebra)
From playlist Fall 2020 Course



