Projective geometry | Geometry
Projective geometry
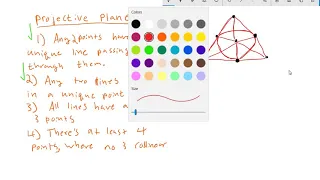
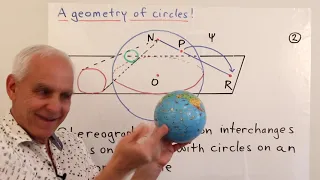
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points (called "points at infinity") to Euclidean points, and vice-versa. Properties meaningful for projective geometry are respected by this new idea of transformation, which is more radical in its effects than can be expressed by a transformation matrix and translations (the affine transformations). The first issue for geometers is what kind of geometry is adequate for a novel situation. It is not possible to refer to angles in projective geometry as it is in Euclidean geometry, because angle is an example of a concept not invariant with respect to projective transformations, as is seen in perspective drawing. One source for projective geometry was indeed the theory of perspective. Another difference from elementary geometry is the way in which parallel lines can be said to meet in a point at infinity, once the concept is translated into projective geometry's terms. Again this notion has an intuitive basis, such as railway tracks meeting at the horizon in a perspective drawing. See projective plane for the basics of projective geometry in two dimensions. While the ideas were available earlier, projective geometry was mainly a development of the 19th century. This included the theory of complex projective space, the coordinates used (homogeneous coordinates) being complex numbers. Several major types of more abstract mathematics (including invariant theory, the Italian school of algebraic geometry, and Felix Klein's Erlangen programme resulting in the study of the classical groups) were motivated by projective geometry. It was also a subject with many practitioners for its own sake, as synthetic geometry. Another topic that developed from axiomatic studies of projective geometry is finite geometry. The topic of projective geometry is itself now divided into many research subtopics, two examples of which are projective algebraic geometry (the study of projective varieties) and projective differential geometry (the study of differential invariants of the projective transformations). (Wikipedia).