Calculus 1 Lecture 3.1: Increasing/Decreasing and Concavity of Functions
Calculus 1 Lecture 3.1: Discussion of Increasing and Decreasing Intervals. Discussion of Concavity of functions.
From playlist Calculus 1 (Full Length Videos)
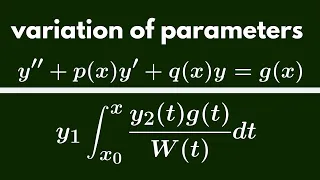
Differential Equations | Variation of Parameters.
We derive the general form for a solution to a differential equation using variation of parameters. http://www.michael-penn.net
From playlist Differential Equations

Statement of Calculus of Variations (6.1)
In this video, I state the calculus of variations problem, and describe how to solve it.
From playlist Intermediate Classical Mechanics

A16 The method of variation of parameters
Starting the derivation for the equation that is used to find the particular solution of a set of differential equations by means of the variation of parameters.
From playlist A Second Course in Differential Equations

The alternating series. Solved problems. Estimating error and partial sum estimation for a set maximum error.
From playlist Advanced Calculus / Multivariable Calculus

The alternating series. Test for convergence.
From playlist Advanced Calculus / Multivariable Calculus

Infinite Limits With Equal Exponents (Calculus)
#Calculus #Math #Engineering #tiktok #NicholasGKK #shorts
From playlist Calculus

Calculus of Variations ft. Flammable Maths
Flammable Maths: https://www.youtube.com/channel/UCtAIs1VCQrymlAnw3mGonhw Leibnitz Rule: https://www.youtube.com/watch?v=wkh1Y7R1sOw This video is an introduction to the calculus of variations. We go over what variational calculus is trying to solve, and derive the Euler-Lagrange equatio
From playlist Analysis

The Palais-Smale Theorem and the Solution of Hilbert’s 23 Problem - Karen Uhlenbeck
Members' Seminar Topic: The Palais-Smale Theorem and the Solution of Hilbert’s 23 Problem Speaker: Karen Uhlenbeck Affiliation: The University of Texas at Austin; Distinguished Visiting Professor, School of Mathematics Date: April 6, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Lec 23 | MIT 18.086 Mathematical Methods for Engineers II
Calculus of Variations / Weak Form View the complete course at: http://ocw.mit.edu/18-086S06 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 18.086 Mathematical Methods for Engineers II, Spring '06

Soviet Era Math Book for Beginners and Mathematical Experts
This book states that it is written with beginners in mind but it can also be of use to expert mathematicians. The first half of the book is on Differential Equations and the second half is on the Calculus of Variations. In this video I will show you this book and I will also solve a diffe
From playlist Book Reviews
A Taste of Calculus of Variations
Dirichlet's Principle In this video, I give you a taste of calculus of variations by illustrating Dirichlet's principle, which says that a function u is a minimizer of a certain Dirichlet energy (kinetic + potential energy) if and only if u solves Poisson's equation. This is a neat way of
From playlist Partial Differential Equations

Karen Uhlenbeck: Some Thoughts on the Calculus of Variations
Abstract: I will talk about some of the classic problems in the calculus of variations, and describe some of the mathematics which was developed to solve them. We will begin with the Greeks and end with some of the tantalizing problems of today. This lecture was given by the 2019 Abel Lau
From playlist Karen K. Uhlenbeck
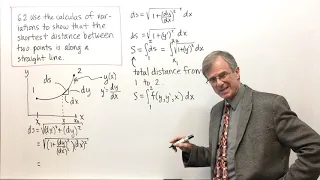
Shortest Distance Between Two Points (6.2)
In this video, I use the calculus of variations to prove that the shortest distance between two points is along a straight line.
From playlist Intermediate Classical Mechanics

Your Daily Equation #19 : At the Core of Fundamental Physics: The Principle of Least Action
Episode 19 #YourDailyEquation: All fundamental laws of physics share a reliance on a single principle: The Principle of Least Action. In this episode of Your Daily Equation, Brian Greene explains this principle in the simplest example and shows how it yields the basic laws of motion introd
From playlist Your Daily Equation with Brian Greene

11_4_2 The Derivative of the Composition of Functions
A further look at the derivative of the composition of a multivariable function and a vector function. There are two methods to calculate such a derivative.
From playlist Advanced Calculus / Multivariable Calculus

Options (Lecture 1) by Shashi Jain
Program Summer Research Program on Dynamics of Complex Systems ORGANIZERS: Amit Apte, Soumitro Banerjee, Pranay Goel, Partha Guha, Neelima Gupte, Govindan Rangarajan and Somdatta Sinha DATE : 15 May 2019 to 12 July 2019 VENUE : Madhava hall for Summer School & Ramanujan hall f
From playlist Summer Research Program On Dynamics Of Complex Systems 2019