
Ordered Fields In this video, I define the notion of an order (or inequality) and then define the concept of an ordered field, and use this to give a definition of R using axioms. Actual Construction of R (with cuts): https://youtu.be/ZWRnZhYv0G0 COOL Construction of R (with sequences)
From playlist Real Numbers

RA1.3. Peano Axioms and Induction
Real Analysis: We consider the Peano Axioms, which are used to define the natural numbers. Special attention is given to Mathematical Induction and the Well-Ordering Principle for N. (Included is an example of how to show a triple equivalence.)
From playlist Real Analysis

What's so wrong with the Axiom of Choice ?
One of the Zermelo- Fraenkel axioms, called axiom of choice, is remarkably controversial. It links to linear algebra and several paradoxes- find out what is so strange about it ! (00:22) - Math objects as sets (00:54) - What axioms we use ? (01:30) - Understanding axiom of choice (03:2
From playlist Something you did not know...

Difficulties with real numbers as infinite decimals ( I) | Real numbers + limits Math Foundations 91
There are three quite different approaches to the idea of a real number as an infinite decimal. In this lecture we look carefully at the first and most popular idea: that an infinite decimal can be defined in terms of an infinite sequence of digits appearing to the right of a decimal point
From playlist Math Foundations

The Banach Tarski paradox - is it nonsense? | Sociology and Pure Mathematics | N J Wildberger
One of the famous "paradoxes" of 20th century pure mathematics is the assertion that it is possible to subdivide a solid ball of radius 1 in three dimensional space into 5 disjoint pieces, take those five pieces and subject them to rigid motions, that is rotations and translations, to obta
From playlist Sociology and Pure Mathematics

Kurt Gödel Centenary - Part III
John W. Dawson, Jr. Pennsylvania State University November 17, 2006 More videos on http://video.ias.edu
From playlist Kurt Gödel Centenary

Construction of Natural Numbers In this, I rigorously define the concept of a natural number, using Peano's axioms. I also explain why those axioms are the basis for the principle of mathematical induction. Enjoy! Check out my Real Numbers Playlist: https://www.youtube.com/playlist?list=
From playlist Real Numbers

How the Axiom of Choice Gives Sizeless Sets | Infinite Series
Viewers like you help make PBS (Thank you 😃) . Support your local PBS Member Station here: https://to.pbs.org/donateinfi Does every set - or collection of numbers - have a size: a length or a width? In other words, is it possible for a set to be sizeless? This in an updated version of our
From playlist An Infinite Playlist

The Mathematical Truth | Enrico Bombieri
Enrico Bombieri, Professor Emeritus, School of Mathematics, Institute for Advanced Study http://www.ias.edu/people/faculty-and-emeriti/bombieri October 29, 2010 In this lecture, Professor Enrico Bombieri attempts to give an idea of the numerous different notions of truth in mathematics.
From playlist Mathematics

Live CEOing Ep 401: Language Design in Wolfram Language [AxiomaticTheory, Echo, FoldWhile, & More]
In this episode of Live CEOing, Stephen Wolfram reviews the design of upcoming functionality for the Wolfram Language. If you'd like to contribute to the discussion in future episodes, you can participate through this YouTube channel or through the official Twitch channel of Stephen Wolfra
From playlist Behind the Scenes in Real-Life Software Design

I introduce the basic Properties of Real Numbers: Commutative Property of Addition and Multiplication, Associative Property of Addition and Multiplication, Identity Property of Multiplication, Identity Property of Addition, Zero Product Property, and Multiplying by Negative One. I also d
From playlist Algebra 1

Axiomatics and the least upper bound property (I1) | Real numbers and limits Math Foundations 121
Here we continue explaining why the current use of `axiomatics' to try to formulate a theory of `real numbers' is fundamentally flawed. We also clarify the layered structure of the rational numbers: we have seen these several times already in prior discussion of the Stern- Brocot tree, her
From playlist Math Foundations

Logic: The Structure of Reason
As a tool for characterizing rational thought, logic cuts across many philosophical disciplines and lies at the core of mathematics and computer science. Drawing on Aristotle’s Organon, Russell’s Principia Mathematica, and other central works, this program tracks the evolution of logic, be
From playlist Logic & Philosophy of Mathematics
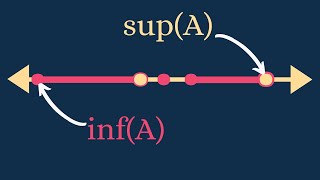
Real Analysis | The Supremum and Completeness of ℝ
We look at the notions of upper and lower bounds as well as least upper bounds and greatest lower bounds of sets of real numbers. We also prove an important classification lemma of least upper bounds. Finally, the completeness axiom of the real numbers is presented. Please Subscribe: ht
From playlist Real Analysis

The Axiom of Choice and Sets | #some2
The axiom of choice is a powerful tool and underlies a lot of mathematics. But what is this tool? How can we use it? And what do we need to do to get there? Find out more in this video by Proffesional Math LLC! Made for SoME2. More info at https://youtu.be/hZuYICAEN9Y #some2
From playlist Summer of Math Exposition 2 videos

Infinities and Skepticism in Mathematics: Steve Patterson interviews N J Wildberger
In this special video, Steve Patterson interviews N J Wildberger on a range of foundational issues exploring infinities and the role of skepticism in modern mathematics. Steve is a philosopher who runs a popular podcast called Patterson in Pursuit, and you can find more of his work at htt
From playlist MathSeminars
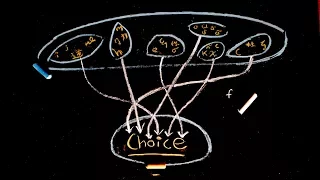
Choice Functions & The Axiom of Choice | Nathan Dalaklis
The Axiom of Choice is often stated in an equivalent form; the Cartesian product of a collection of non-empty sets is non-empty, however, what is the original statement, and what does it have to do with functions? Also, what is a choice function? In this discussion of the axiom of choice,
From playlist The First CHALKboard

Proof: Archimedean Principle of Real Numbers | Real Analysis
Given real numbers a and b, where a is positive, we can always find a natural number m so that n*a is greater than b. In other words, we can add a to itself enough times to get a number greater than b. Equivalently, given any real number x, there exists a natural number greater than x, mea
From playlist Real Analysis

Support Vsauce, your brain, Alzheimer's research, and other YouTube educators by joining THE CURIOSITY BOX: a seasonal delivery of viral science toys made by Vsauce! A portion of all proceeds goes to Alzheimer's research and our Inquisitive Fellowship, a program that gives money and resour
From playlist Science
