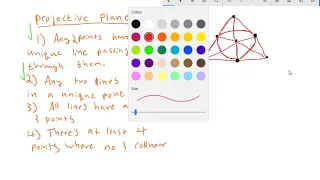
Introduction to Projective Geometry (Part 2)
The second video in a series about projective geometry. We list the axioms for projective planes, give an examle of a projective plane with finitely many points, and define the real projective plane.
From playlist Introduction to Projective Geometry

algebraic geometry 17 Affine and projective varieties
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the relation between affine and projective varieties, with some examples such as a cubic curve and the twisted cubic.
From playlist Algebraic geometry I: Varieties
Calculus and affine geometry of the magical parabola | Algebraic Calc and dCB curves 3 | Wild Egg
Algebraic Calculus naturally lives in affine geometry, not Euclidean geometry. Affine geometry is the geometry of parallelism, or (almost the same thing) --- the geometry of pure linear algebra. The parabola is characterized projectively in this geometry as the unique conic which is tangen
From playlist Algebraic Calculus One Info

algebraic geometry 5 Affine space and the Zariski topology
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the definition of affine space and its Zariski topology.
From playlist Algebraic geometry I: Varieties

Affine and mod-affine varieties in arithmetic geometry. - Charles - Workshop 2 - CEB T2 2019
François Charles (Université Paris-Sud) / 24.06.2019 Affine and mod-affine varieties in arithmetic geometry. We will explain how studying arithmetic versions of affine schemes and their bira- tional modifications leads to a generalization to arbitrary schemes of both Fekete’s theorem on
From playlist 2019 - T2 - Reinventing rational points

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes
Novel Algebraic Operations for Affine Geometry | Algebraic Calculus One | Wild Egg
We introduce some novel conventions to help us set up the foundations of affine geometry. We learn about differences of points, sums of points and vectors, affine combinations and vector proportions. And then use these to state a number of important results from affine geometry, including
From playlist Algebraic Calculus One from Wild Egg
“Closed Geodesics on Surfaces Pt.1” - Nancy Hingston
Nancy Hingston TCNJ “Closed geodesics on surfaces” Tuesday May 17
From playlist Mathematics

algebraic geometry 27 The twisted cubic
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It describes two examples: the twisted cubic is isomorphic to a projective line, and the affine plane without the origin is not isomorphic to any affine algebraic set.
From playlist Algebraic geometry I: Varieties

algebraic geometry 15 Projective space
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It introduces projective space and describes the synthetic and analytic approaches to projective geometry
From playlist Algebraic geometry I: Varieties

Introduction to Elliptic Curves 1 by Anupam Saikia
PROGRAM : ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (ONLINE) ORGANIZERS : Ashay Burungale (California Institute of Technology, USA), Haruzo Hida (University of California, Los Angeles, USA), Somnath Jha (IIT - Kanpur, India) and Ye Tian (Chinese Academy of Sciences, China) DA
From playlist Elliptic Curves and the Special Values of L-functions (ONLINE)
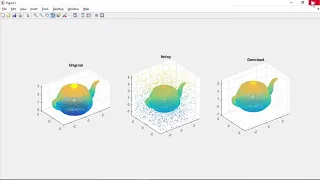
Point Clouds | Student Competition: Computer Vision Training
In this video, you will learn about point clouds and how to work with them in MATLAB. Get files: https://bit.ly/2ZBy0q2 Explore the MATLAB and Simulink Robotics Arena: https://bit.ly/2yIgwfS --------------------------------------------------------------------------------------------------
From playlist Student Competition: Computer Vision Training

Affine Combinations and Barycentric Coords | Algebraic Calculus One | Wild Egg
In this video we show how affine combinations and barycentric coordinates express mathematically what Archimedes' Law of the Lever captures in terms of the centre of mass of a triangle. We examine both the one dimensional case of a segment, as well as the more general two dimensional case
From playlist Algebraic Calculus One from Wild Egg

Tropical Geometry - Lecture 11 - Toric Varieties | Bernd Sturmfels
Twelve lectures on Tropical Geometry by Bernd Sturmfels (Max Planck Institute for Mathematics in the Sciences | Leipzig, Germany) We recommend supplementing these lectures by reading the book "Introduction to Tropical Geometry" (Maclagan, Sturmfels - 2015 - American Mathematical Society)
From playlist Twelve Lectures on Tropical Geometry by Bernd Sturmfels

Elliptic Curves - Lecture 4a - Varieties, function fields, dimension
This video is part of a graduate course on elliptic curves that I taught at UConn in Spring 2021. The course is an introduction to the theory of elliptic curves. More information about the course can be found at the course website: https://alozano.clas.uconn.edu/math5020-elliptic-curves/
From playlist An Introduction to the Arithmetic of Elliptic Curves
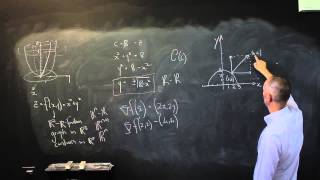
11_6_1 Contours and Tangents to Contours Part 1
A contour is simply the intersection of the curve of a function and a plane or hyperplane at a specific level. The gradient of the original function is a vector perpendicular to the tangent of the contour at a point on the contour.
From playlist Advanced Calculus / Multivariable Calculus

This lecture gives an introductory overview of the Chow ring of a nonsingular variety. The idea is to define a ring structure related to subvarieties with the product corresponding to intersection. There are several complications that have to be solved, in particular how to define intersec
From playlist Algebraic geometry: extra topics