Affine plane (incidence geometry)
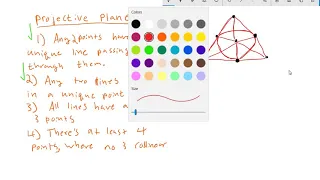
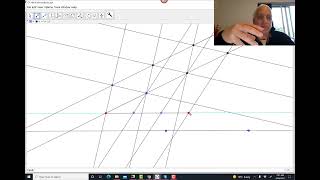
In geometry, an affine plane is a system of points and lines that satisfy the following axioms: * Any two distinct points lie on a unique line. * Given any line and any point not on that line there is a unique line which contains the point and does not meet the given line. (Playfair's axiom) * There exist three non-collinear points (points not on a single line). In an affine plane, two lines are called parallel if they are equal or disjoint. Using this definition, Playfair's axiom above can be replaced by: * Given a point and a line, there is a unique line which contains the point and is parallel to the line. Parallelism is an equivalence relation on the lines of an affine plane. Since no concepts other than those involving the relationship between points and lines are involved in the axioms, an affine plane is an object of study belonging to incidence geometry. They are non-degenerate linear spaces satisfying Playfair's axiom. The familiar Euclidean plane is an affine plane. There are many finite and infinite affine planes. As well as affine planes over fields (and division rings), there are also many non-Desarguesian planes, not derived from coordinates in a division ring, satisfying these axioms. The Moulton plane is an example of one of these. (Wikipedia).