
Driving Downtown - Los Angeles Movie Set 4K - USA
Driving Downtown Highlights - Episode 1. Location shooting is the shooting of a film or television production in a real-world setting rather than a sound stage or backlot. The location may be interior or exterior. The filming location may be the same in which the story is set (for example
From playlist Location by Country - United States of America - J Utah

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
definition of adjacent angles
From playlist Common Core Standards - 8th Grade

👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure
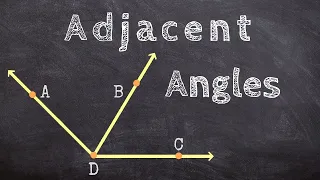
What are examples of adjacent angles
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

What is an angle and it's parts
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

What are adjacent angles and linear pairs
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

CCSS What is the Angle Addition Postulate
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

What is a Manifold? Lesson 6: Topological Manifolds
Topological manifolds! Finally! I had two false starts with this lesson, but now it is fine, I think.
From playlist What is a Manifold?

Lie Groups and Lie Algebras: Lesson 36 - Review of continuity and homeomorphisms
Lie Groups and Lie Algebras: Lesson 36 - Review of continuity and homeomorphisms This is a review lesson regarding the topological definition of continuity, homeomorphism, and topological properties. This is important because the Fundamental group of a topological space is a topological
From playlist Lie Groups and Lie Algebras

Jens Hemelaer: Toposes in arithmetic noncommutative geometry
Talk by Jens Hemelaer in Global Noncommutative Geometry Seminar (Americas) on February 5, 2021
From playlist Global Noncommutative Geometry Seminar (Americas)

Local rigidity and C^0 symplectic and contact topology - Mike Usher
Symplectic Dynamics/Geometry Seminar Topic: Local rigidity and C^0 symplectic and contact topology Speaker: Mike Usher Affiliation: University of Georgia Date: November 11, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

G. Walsh - Boundaries of Kleinian groups
We study the problem of classifying Kleinian groups via the topology of their limit sets. In particular, we are interested in one-ended convex-cocompact Kleinian groups where each piece in the JSJ decomposition is a free group, and we describe interesting examples in this situation. In ce
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie

Parallel session 9 by Jean-Francois Lafont
Geometry Topology and Dynamics in Negative Curvature URL: https://www.icts.res.in/program/gtdnc DATES: Monday 02 Aug, 2010 - Saturday 07 Aug, 2010 VENUE : Raman Research Institute, Bangalore DESCRIPTION: This is An ICM Satellite Conference. The conference intends to bring together ma
From playlist Geometry Topology and Dynamics in Negative Curvature

Barcodes for Hamiltonian homeomorphisms of surfaces -Benoît Joly
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Barcodes for Hamiltonian homeomorphisms of surfaces Speaker: Benoît Joly Affiliation: Ruhr-Universität Bochum Date: March 25, 2022 In this talk, we will study the Floer Homology barcodes from a dynamical poin
From playlist Mathematics

Diffeomorphism Groups of Critical Regularity (Lecture 4) by Sang-hyun Kim
PROGRAM: PROBABILISTIC METHODS IN NEGATIVE CURVATURE ORGANIZERS: Riddhipratim Basu (ICTS - TIFR, India), Anish Ghosh (TIFR, Mumbai, India), Subhajit Goswami (TIFR, Mumbai, India) and Mahan M J (TIFR, Mumbai, India) DATE & TIME: 27 February 2023 to 10 March 2023 VENUE: Madhava Lecture Hall
From playlist PROBABILISTIC METHODS IN NEGATIVE CURVATURE - 2023

Sebastian Hensel: Fine curve graphs and surface homeomorphisms
CONFERENCE Recording during the thematic meeting : "Big Mapping Class Group and Diffeomorphism Groups " the October 10, 2022 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mat
From playlist Dynamical Systems and Ordinary Differential Equations

Diffeomorphism groups of critical regularity by Sang-hyun Kim
PROGRAM: PROBABILISTIC METHODS IN NEGATIVE CURVATURE ORGANIZERS: Riddhipratim Basu (ICTS - TIFR, India), Anish Ghosh (TIFR, Mumbai, India), Subhajit Goswami (TIFR, Mumbai, India) and Mahan M J (TIFR, Mumbai, India) DATE & TIME: 27 February 2023 to 10 March 2023 VENUE: Madhava Lecture Hall
From playlist PROBABILISTIC METHODS IN NEGATIVE CURVATURE - 2023

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
