
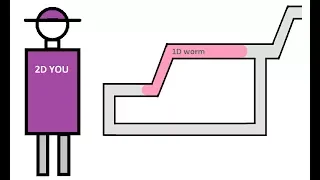
WHEN SPACE DOES NOT HAVE DISTANCE: What is the Long Line in Math and Other Examples (Version 2.0)
In many ways metric spaces grant a large amount of structure to a topological space. So it's natural to ask what happens when space does not have distance defined on it. Can we still talk about things like size or even compare these types of spaces to other metrizable spaces? The answer is
From playlist The New CHALKboard

Is there any place in the Universe where there's truly nothing? Consider the gaps between stars and galaxies? Or the gaps between atoms? What are the properties of nothing?
From playlist Guide to Space

What exactly is space? Brian Greene explains what the "stuff" around us is. Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https:
From playlist Science Unplugged: Physics

Is The Universe Perfect For Life? Understanding the Anthropic Principle
Doesn't it feel like the Universe is perfectly tuned for life? Actually, it's a horrible hostile place, delivering the bare minimum for human survival. Support us at: http://www.patreon.com/universetoday More stories at: http://www.universetoday.com/ Follow us on Twitter: @universetoday Fo
From playlist Guide to Space

Sergey Melikhov, Steklov Math Institute (Moscow) Title: Fine Shape Abstract: A shape theory is something which is supposed to agree with homotopy theory on polyhedra and to treat more general spaces by looking at their polyhedral approximations. Or if you prefer, it is something which is s
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Is the nothing of a black hole the same as empty space?
Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https://twitter.com/worldscienceu
From playlist Science Unplugged: Black Holes

The Human Body in Space - What happens to your body in space? Start learning with Brilliant today for FREE: http://brilliant.org/aperture Follow me on Instagram: https://www.instagram.com/mcewen/ Space is the final frontier. But you know, it’s not like space has a lot going on. There is q
From playlist Science & Technology 🚀

Topology PhD Qualifying Exam Problems (Stream 1)
Just practicing some arguments from topology qualifying exam problems. A few folks said they wanted me to hang out here instead of on Twitch today. 00:00:00 Dead Air 00:00:53 I exist huzzah! 00:09:26 Continuous Images of Metric Spaces in Hausdorff Spaces Problem 01:13:45 Separable First C
From playlist CHALK Streams

Vera Tonic - Alternative proofs for the n-dimensional resolution theorems
Vera Tonic, University of Rijeka, Croatia Title: Alternative proofs for the n-dimensional resolution theorems Abstract: We present new, unified proofs for the cell-like-, Z/p-, and Q-resolution theorems in extension theory. Our arguments employ extensions that are much simpler than those u
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021

Henry Adams (3/12/21): Vietoris-Rips thickenings: Problems for birds and frogs
An artificial distinction is to describe some mathematicians as birds, who from their high vantage point connect disparate areas of mathematics through broad theories, and other mathematicians as frogs, who dig deep into particular problems to solve them one at a time. Neither type of math
From playlist Vietoris-Rips Seminar

Dustin Clausen: New foundations for functional analysis
Talk by Dustin Clausen in Global Noncommutative Geometry Seminar (Americas) on November 12, 2021.
From playlist Global Noncommutative Geometry Seminar (Americas)

Ask the Space Lab Expert: What is Space?
Have you ever wanted to go to Space? In this first episode of Space Lab, Brad and Liam from "World of the Orange" take you on an adventure to discover exactly what is Space. You'll find out about the solar system, the big bang, Sci-Fi movies that are becoming reality, and more!
From playlist What is Space? YouTube Space Lab with Liam and Brad
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

If the universe is spatially infinite, what can we say about reality...
Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https://twitter.com/worldscienceu
From playlist Science Unplugged: Cosmology

David Rosenthal - Finitely F-amenable actions and decomposition complexity of groups
38th Annual Geometric Topology Workshop (Online), June 15-17, 2021 David Rosenthal, St. John's University Title: Finitely F-amenable actions and decomposition complexity of groups Abstract: In their groundbreaking work on the Farrell-Jones Conjecture for Gromov hyperbolic groups, Bartels
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021
J. Bruinier et J. Ignacio Burgos Gil - Arakelov theory on Shimura varieties (part1)
A Shimura variety is a higher-dimensional analogue of a modular curve that arises as a quotient of a Hermitian symmetric space by a congruence subgroup of a reductive algebraic group defined over Q. Shimura varieties have a very rich geometric and arithmetic structure. For instance they ar
From playlist Ecole d'été 2017 - Géométrie d'Arakelov et applications diophantiennes

Henry Adams (5/1/21): Bridging applied and quantitative topology
I will survey emerging connections between applied topology and quantitative topology. Vietoris-Rips complexes were invented by Vietoris in order to define a (co)homology theory for metric spaces, and by Rips for use in geometric group theory. More recently, they have found applications in
From playlist TDA: Tutte Institute & Western University - 2021

Open and closed sets -- Proofs
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

J. Bruinier et J. Ignacio Burgos Gil - Arakelov theory on Shimura varieties (part2)
A Shimura variety is a higher-dimensional analogue of a modular curve that arises as a quotient of a Hermitian symmetric space by a congruence subgroup of a reductive algebraic group defined over Q. Shimura varieties have a very rich geometric and arithmetic structure. For instance they ar
From playlist Ecole d'été 2017 - Géométrie d'Arakelov et applications diophantiennes