Computational problems in graph theory | Graph theory | Extensions and generalizations of graphs | NP-complete problems | NP-hard problems | Graph coloring
Graph coloring
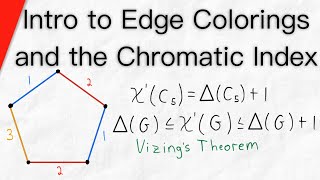
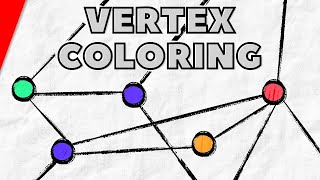
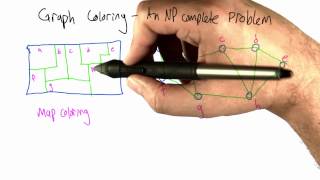
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex coloring of its dual. However, non-vertex coloring problems are often stated and studied as-is. This is partly pedagogical, and partly because some problems are best studied in their non-vertex form, as in the case of edge coloring. The convention of using colors originates from coloring the countries of a map, where each face is literally colored. This was generalized to coloring the faces of a graph embedded in the plane. By planar duality it became coloring the vertices, and in this form it generalizes to all graphs. In mathematical and computer representations, it is typical to use the first few positive or non-negative integers as the "colors". In general, one can use any finite set as the "color set". The nature of the coloring problem depends on the number of colors but not on what they are. Graph coloring enjoys many practical applications as well as theoretical challenges. Beside the classical types of problems, different limitations can also be set on the graph, or on the way a color is assigned, or even on the color itself. It has even reached popularity with the general public in the form of the popular number puzzle Sudoku. Graph coloring is still a very active field of research. Note: Many terms used in this article are defined in Glossary of graph theory. (Wikipedia).