Computational problems in graph theory | NP-complete problems
Clique problem
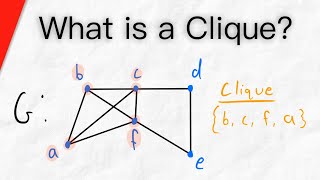
In computer science, the clique problem is the computational problem of finding cliques (subsets of vertices, all adjacent to each other, also called complete subgraphs) in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique (a clique with the largest possible number of vertices), finding a maximum weight clique in a weighted graph, listing all maximal cliques (cliques that cannot be enlarged), and solving the decision problem of testing whether a graph contains a clique larger than a given size. The clique problem arises in the following real-world setting. Consider a social network, where the graph's vertices represent people, and the graph's edges represent mutual acquaintance. Then a clique represents a subset of people who all know each other, and algorithms for finding cliques can be used to discover these groups of mutual friends. Along with its applications in social networks, the clique problem also has many applications in bioinformatics, and computational chemistry. Most versions of the clique problem are hard. The clique decision problem is NP-complete (one of Karp's 21 NP-complete problems). The problem of finding the maximum clique is both fixed-parameter intractable and hard to approximate. And, listing all maximal cliques may require exponential time as there exist graphs with exponentially many maximal cliques. Therefore, much of the theory about the clique problem is devoted to identifying special types of graph that admit more efficient algorithms, or to establishing the computational difficulty of the general problem in various models of computation. To find a maximum clique, one can systematically inspect all subsets, but this sort of brute-force search is too time-consuming to be practical for networks comprising more than a few dozen vertices.Although no polynomial time algorithm is known for this problem, more efficient algorithms than the brute-force search are known. For instance, the Bron–Kerbosch algorithm can be used to list all maximal cliques in worst-case optimal time, and it is also possible to list them in polynomial time per clique. (Wikipedia).