Curvature (mathematics) | Differential geometry of surfaces | Surfaces | Differential geometry | Differential topology
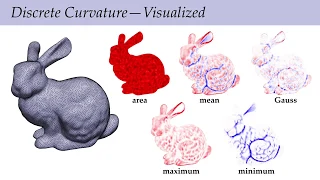
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature Κ of a surface at a point is the product of the principal curvatures, κ1 and κ2, at the given point: The Gaussian radius of curvature is the reciprocal of Κ.For example, a sphere of radius r has Gaussian curvature 1/r2 everywhere, and a flat plane and a cylinder have Gaussian curvature zero everywhere. The Gaussian curvature can also be negative, as in the case of a hyperboloid or the inside of a torus. Gaussian curvature is an intrinsic measure of curvature, depending only on distances that are measured “within” or along the surface, not on the way it is isometrically embedded in Euclidean space. This is the content of the Theorema egregium. Gaussian curvature is named after Carl Friedrich Gauss, who published the Theorema egregium in 1827. (Wikipedia).