Metric tensor

Riemannian geometry | Differential geometry | Metric tensors | Tensors

In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold M (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p (that is, a bilinear function that maps pairs of tangent vectors to real numbers), and a metric tensor on M consists of a metric tensor at each point p of M that varies smoothly with p. A metric tensor g is positive-definite if g(v, v) > 0 for every nonzero vector v. A manifold equipped with a positive-definite metric tensor is known as a Riemannian manifold. Such a metric tensor can be thought of as specifying infinitesimal distance on the manifold. On a Riemannian manifold M, the length of a smooth curve between two points p and q can be defined by integration, and the distance between p and q can be defined as the infimum of the lengths of all such curves; this makes M a metric space. Conversely, the metric tensor itself is the derivative of the distance function (taken in a suitable manner). While the notion of a metric tensor was known in some sense to mathematicians such as Carl Gauss from the early 19th century, it was not until the early 20th century that its properties as a tensor were understood by, in particular, Gregorio Ricci-Curbastro and Tullio Levi-Civita, who first codified the notion of a tensor. The metric tensor is an example of a tensor field. The components of a metric tensor in a coordinate basis take on the form of a symmetric matrix whose entries transform covariantly under changes to the coordinate system. Thus a metric tensor is a covariant symmetric tensor. From the coordinate-independent point of view, a metric tensor field is defined to be a nondegenerate symmetric bilinear form on each tangent space that varies smoothly from point to point. (Wikipedia).

What is General Relativity? Lesson 68: The Einstein Tensor

What is General Relativity? Lesson 68: The Einstein Tensor The Einstein tensor defined! Using the Ricci tensor and the curvature scalar we can calculate the curvature scalar of a slice of a manifold using the Einstein tensor. Please consider supporting this channel via Patreon: https:/

From playlist What is General Relativity?

What is a Tensor? Lesson 11: The metric tensor

What is a Tensor 11: The Metric Tensor

From playlist What is a Tensor?

The Maths of General Relativity (4/8) - Metric tensor

In this series, we build together the theory of general relativity. This fourth video focuses on the notion of metric tensor, its relations to the Christoffel symbols, and physical distances. For more videos, subscribe to the YouTube channel : https://www.youtube.com/ScienceClicEN And if

From playlist The Maths of General Relativity

What is a Tensor? Lesson 17: The covariant derivative (elementary pedagogy)

From playlist What is a Tensor?

Tensor Calculus For Physics Majors 006 | The Metric Tensor pt. 1

Today I talk about the metric tensor and how it relates coordinate displacement to distance. I also show how to calculate the components of the metric tensor in spherical coordinates. Link to Tensor Calculus for Physics Book: https://www.amazon.com/gp/product/1421415658/ref=as_li_tl?ie=UT

From playlist New To Tensors? Start Here

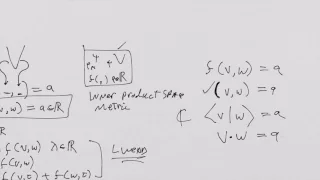
What is a Tensor 10: Metric spaces

From playlist What is a Tensor?

Relativity 7b2 - metric tensor details

Some details regarding the metric tensor that we will use in the next appendix video.

From playlist Relativity - appendix videos

What is General Relativity? Lesson 48: Ricci tensor and conformal transformations

What is General Relativity? Lesson 48: Ricci tensor and conformal transformations We introduce the Ricci tensor, curvature scalar, and begin the difficult derivation of the Weyl tensor. Please consider supporting this channel via Patreon: https://www.patreon.com/XYLYXYLYX and discussin

From playlist What is General Relativity?

What is a metric space ?

Metric space definition and examples. Welcome to the beautiful world of topology and analysis! In this video, I present the important concept of a metric space, and give 10 examples. The idea of a metric space is to generalize the concept of absolute values and distances to sets more gener

From playlist Topology

Tensor Calculus 4b: Position Vector, Covariant Basis, Covariant Metric Tensor, Contravariant Basis

This course will eventually continue on Patreon at http://bit.ly/PavelPatreon Textbook: http://bit.ly/ITCYTNew Errata: http://bit.ly/ITAErrata McConnell's classic: http://bit.ly/MCTensors Table of Contents of http://bit.ly/ITCYTNew Rules of the Game Coordinate Systems and the Role of Te

From playlist Introduction to Tensor Calculus

The Einstein Field Equations | Tensor Calc Finale

Today we use all the tools we've got in our back pocket to "derive" the Einstein Field Equations of general relativity. It's more of a motivation than a derivation, I suppose. This series is based off the book "Tensor Calculus for Physics" by Dwight Neuenschwander: https://amzn.to/3rEema3

From playlist New To Tensors? Start Here

Tensor Calculus 4g: Index Juggling

From playlist Introduction to Tensor Calculus

What is General Relativity? Lesson 37: The line element

What is General Relativity? Lesson 37: The line element This is a repost of Lesson 37 shortened and with some corrections. We introduce the origin of the "line element" and begin our exploration of spherical symmetry. Note the indexing error when I wrote down the equation for the connec

From playlist What is General Relativity?

Helvi Witek - Tutorial: 3+1 decomposition with xTensor - IPAM at UCLA

Recorded 20 September 2021. Helvi Witek of the University of Illinois presents "Tutorial: 3+1 decomposition with xTensor" at IPAM's Mathematical and Computational Challenges in the Era of Gravitational Wave Astronomy Tutorial. Abstract: The open-source xAct suite is a powerful tool for ten

From playlist Tutorials: Math & Computational Challenges in the Era of Gravitational Wave Astronomy

xAct: Efficient Tensor Computer Algebra: Live with the R&D team

Presentation begins at 1:43 In this stream, we have xAct: Efficient Tensor Computer Algebra with Wolfram R&D. Follow us on our official social media channels. Twitter: https://twitter.com/WolframResearch/ Facebook: https://www.facebook.com/wolframresearch/ Instagram: https://www.instagra

From playlist Live with the R&D Team

Tensor Calculus For Physics Ep 8| The Metric pt. 3 |Covariant and Contravariant Vectors

Today I go over converting between vectors and their duals, transformations of covariant tensors, proving the metric is a tensor, covariant/contravariant vectors, tensor algebra, and relating the Jacobian to the metric! For visualizing covariant/contravariant vectors and just a great expl

From playlist New To Tensors? Start Here

Introduction to Metric Spaces

Introduction to Metric Spaces - Definition of a Metric. - The metric on R - The Euclidean Metric on R^n - A metric on the set of all bounded functions - The discrete metric

From playlist Topology

Einstein's General Theory of Relativity | Lecture 4

October 13, 2008, Stanford's Felix Bloch Professor of Physics, Leonard Susskind, discusses covariant and contra variant indices, tensor arithmetic, algebra and calculus, and the geometry of expanding space time. This Stanford Continuing Studies course is the fourth of a six-quarter sequ

From playlist Lecture Collection | Modern Physics: Einstein's Theory

Metric tensor

Related pages